Chapter 3 Finite Markov Decision Processes
“Reinforcement Learning: An Introduction” by Richard Sutton & Andrew Barto, 2nd Ed
Author: Charles Zhang
All Notes Catelog for Reinforcement Learning: An Introduction. This post is created following BY-NC-ND 4.0 agreement, please follow terms while sharing.
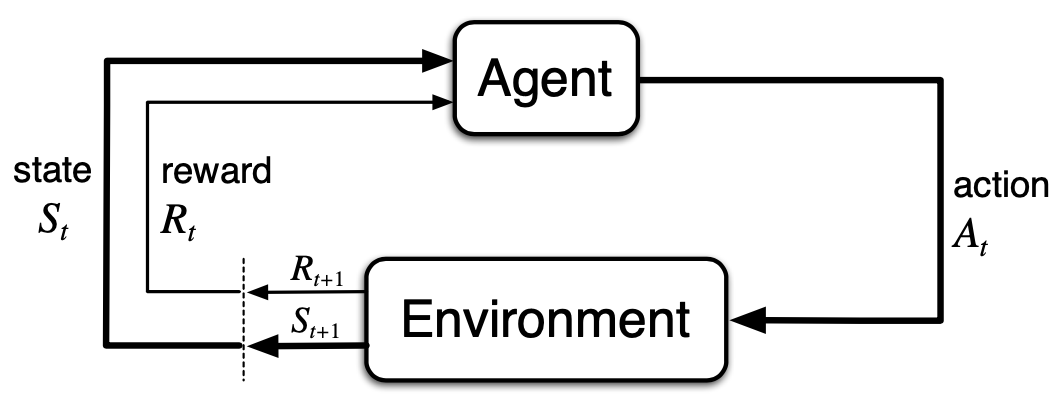
\(S_t \in \mathcal{S}, A_{t} \in \mathcal{A}(s), R_{t+1} = \mathcal{R}\subset \mathbb{R}\rightarrow S_{t+1}\)
squence or trajectory: \(S_0, A_0, S_1, A_1, R_2, S_2, A_2, R_3,...\)
Dynamics of MDP: \(p: \mathcal{S}\times\mathcal{R}\times\mathcal{S}\times\mathcal{A}\): \[ p(s', r|s, a) \doteq \text{Pr}\{S_t=s', R_t=r|S_{t+1}=s, A_{t+1}=a\} \] then \(\displaystyle \sum_{s'\in\mathcal{S}}\sum_{r\in\mathcal{R}}p(s', r|s, a) = 1, \forall s\in \mathcal{S}, a\in\mathcal{A}(s)\). And follows the Markov Property: \(S_t, R_t\) only dependent on \(S_{t-1}, A_{t-1}\).
state-transition probabilities \(p: \mathcal{S}\times\mathcal{S}\times\mathcal{A}\rightarrow [0,1]\) \[ p(s'|s, a) \doteq \text{Pr}\{S_t=s'|S_{t+1}=s, A_{t+1}=a\} = \sum_{r\in\mathcal{R}}p(s', r|s, a) \] \(r: \mathcal{S}\times\mathcal{A}\rightarrow \mathbb{R}\): \[ r(s,a)\doteq \mathbb{E}[R_t|S_{t-1}=s, A_{t-1}=a] = \sum_{r\in\mathcal{R}}r\sum_{s'\in\mathcal{S}}p(s', r|s, a) \] \(r: \mathcal{S}\times\mathcal{A}\times\mathcal{S}\rightarrow \mathbb{R}\): \[ r(s,a, s')\doteq \mathbb{E}[R_t|S_{t-1}=s, A_{t-1}=a, S_t=s'] = \sum_{r\in\mathcal{R}}r\frac{p(s', r|s, a)}{p(s'|s, a)} \] Agent Goal: maximize the cumulative reward \(\Rightarrow\) maximize expected return: \[ G_t \doteq \sum_{i=t+1}^{T} R_i, \text{ }\text{ }T\text{ is final time step} \] Episodic tasks: reset after the terminal state\(\mathcal{S}^+\): \(\mathcal{S}+\mathcal{S}^+\)
Continuing tasks: \(T=\infty\)
Discounted rate \(\gamma\): \[\displaystyle G_t\doteq \sum_{k=0}^{\infty}\gamma^k R_{t+k+1}, \gamma\in(0,1)\] and therefore: \[\displaystyle G_t\doteq R_{t+1}+\gamma G_{t+1}\] if reward is constant: \(G_t = \displaystyle \frac{r}{1-r}\)
Meaning: \(k\) time steps in the future is worth only \(\gamma^{k-1}\) times what it would be worth if it is received immediately.
\(\gamma\rightarrow 1\): takes future rewards into account more strongly.
Policy \(\pi(a|s) = P(A_t=a|S_t=s)\)
Value functions
\(v_\pi(s)\): state-value function for policy \(\pi\) for MDP: \[ v_\pi(s) \doteq \mathbb{E}[G_t|S_t=s] = \mathbb{E}_\pi \left[\sum_{k=1}^\infty \gamma^k R_{t+k+1}| S_t=s\right] \] \(q_\pi(s)\): action-value function for policy \(\pi\) for MDP: \[ v_\pi(s) \doteq \mathbb{E}[G_t|S_t=s, A_t=a] = \mathbb{E}_\pi \left[\sum_{k=1}^\infty \gamma^k R_{t+k+1}| S_t=s,A_t=a\right] \] Bellman Equation for \(v_\pi\) (recursive relationship): \[ v_\pi(s) = \sum_{a} \pi(a | s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right], \forall s\in \mathcal{S} \] Proof:
Consider: \(\displaystyle \mathbb{E}_\pi[R_{t+1}|S_t=s] = \sum_r p(r|s)r = \sum_{s'} \sum_{a} \sum_{r} p(s'a,r|s)r = \sum_{s'} \sum_{a} \sum_{r} \pi(a|s)p(s',r|s,a)r \), and: \(\displaystyle \mathbb{E}_\pi[v_\pi(S_{t+1})|S_t=s] = \sum_a\pi(a|s)\sum_{s'}\sum_rp(s',r|s,a) v_\pi(s')\), we have: \[ \begin{aligned} v_{\pi}(s) &=\mathbb{E}_{\pi}\left[G_{t} | S_{t}=s\right] \\ &=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma G_{t+1} | S_{t}=s\right] \\ &=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma \mathbb{E}_{\pi}\left[G_{t+1} | S_{t+1}\right] | S_{t}=s\right] \text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{(by Law of iterated expectation)}\\ &=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) | S_{t}=s\right] \\ &=\sum_{a} \pi(a | s) \sum_{r} \sum_{s^{\prime}} p\left(s^{\prime}, r | s, a\right) r+\gamma \sum_{a} \pi(a | s) \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r | s, a\right) v_{\pi}\left(s^{\prime}\right) \\ &=\sum_{a} \pi(a | s) \sum_{s'} \sum_{r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right] \\ &= \sum_{a} \pi(a | s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right], \forall s\in \mathcal{S} \end{aligned} \] Similarly, we have the bellman equation for \(q_\pi(s,a)\): \[ q_{\pi}(s, a)\doteq \mathbb{E}_\pi[G_t|S_t=s, A_t=a]=\sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right] \] and therefore, \[ v_\pi(s)=\sum_a\pi(a|s)q_\pi(s,a) \]
The backup diagrams below provide the better understanding to the bellman equation.
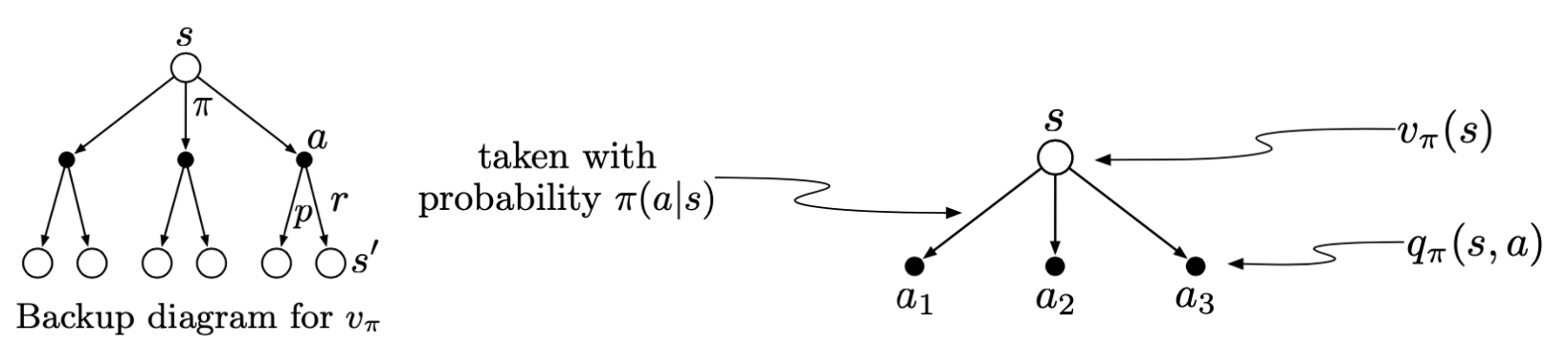
A fun fact about the reward for the value function:
if \(r\rightarrow r+c, c\in\mathbb{R}\), then \(v_\pi(s)\rightarrow v_\pi(s)+\displaystyle \frac{v}{1-\gamma}, \gamma\in[0,1)\).
Proof:
\(\displaystyle \begin{aligned}v_\pi^{\text{old}} (s) &= \mathbb{E}_\pi\left[ \sum_{k=0}^\infty \gamma^k R_{t+k+1} |S_t=s \right] \\ v_\pi^{\text{new}}(s) &= \mathbb{E}_\pi\left[ \sum_{k=0}^\infty \gamma^k \left(R_{t+k+1}+c\right) |S_t=s \right]\\ &= \mathbb{E}_\pi\left[ \sum_{k=0}^\infty \gamma^k R_{t+k+1} |S_t=s \right] + \sum_{k=0}^\infty \gamma^k \cdot c \\ &= v_\pi^{\text{old}}(s) + c\cdot\frac{1}{1-\gamma},\text{ } \text{ }\forall s\in\mathcal{S}, \gamma\in[0,1) \end{aligned}\)
Optimal policy and value functions: \[ v_*(s)\doteq \max_\pi v_\pi(s) = \max_a \sum_{s',r}p(s',r|s,a)[r+\gamma v_*(s')], \text{ } \forall s\in\mathcal{S} \] \[ q_*(s,a)\doteq \max_\pi q_\pi(s,a) = \sum_{s',r}p(s', r|s,a)[r+\gamma \max_{a'} q_*(s',a')], \text{ } \forall s\in\mathcal{S} \] If there were finite \(n\) states, then there will be \(n\) equations for \(v_*(s)\) since dynamics \(p\) is known and MDP is finite. Then, the best policy could be found by "greedy". However, "optimal" requires extreme computatoinal and memory cost due to the enumerations, so we are looking for approximations.
Greedy Policy \(\pi'(s) = \arg\max_x q_\pi(s,a)\)
Efficiency: search directly: \(O(k^n)\) with n states k actions; dynamic programing: \(O(c^n, c^k)\), with constant c, which will be introduced in the next section.
Implementation of Stochastic GridWorld¶

Using Bellman Optimality Equation: $v*(s) = \max_a \{\sum_{s',r} p(s', r\mid s, a)\cdot [r + \gamma \cdot v(s')]\} = \max q_{\pi*}(s, a)$

The explanations, use of equations, and details for implementation are all detailed commented in the code below.
"""
--------------------------
Environment
c 0 1 2 3
r - - - - - - - - - -
0 | | | | +1 |
- - - - - - - - - -
1 | |WALL| | -1 |
- - - - - - - - - -
2 | | | | |
- - - - - - - - - -
For Visualization:
- - - - - - - - - -
3 | | | | +1 |
- - - - - - - - - -
2 | |WALL| | -1 |
- - - - - - - - - -
1 | | | | |
r - - - - - - - - - -
c 1 2 3 4
@author: Charles Zhang
@date Mar 28, 2021
---------------------------
"""
import numpy as np
from matplotlib.table import Table
import matplotlib.pyplot as plt
# Grid Environment for MDP Value Iteration
class GridWorldEnv:
EXIT = (float("inf"), float("inf"))
# actions
NORTH = (-1, 0)
EAST = (0, 1)
SOUTH = (1, 0)
WEST = (0, -1)
ACTIONS = [NORTH, EAST, SOUTH, WEST]
index = {NORTH: 0, EAST: 1, SOUTH: 2, WEST: 3, EXIT: -1}
GAMEOVER = (-1, -1) # by convenience, the next state of terminals is (-1, -1)
def __init__(self, shape, prob, walls, terminals, alive_reward=0.0):
"""
:param shape: shape of gridworld: (row, col)
:param prob: probability to go north(for stochastic move)
:param walls: list of walls: [(1, 1)] if only one wall at (1, 1)
:param terminals: dictionary of goal and death terminal states with reward
{(0, 3): +1, (1, 3): -1} in this problem
:param alive_reward: alive reward
"""
self.rows, self.cols = shape
p_not_north = (1 - prob) / 2
self.turns = {-1: p_not_north, 0: prob, 1: p_not_north} # turn west, north, or east
self.walls = set(walls)
self.terminals = terminals
self.alive_reward = alive_reward
def getStates(self):
"""
All available states(all states except wall(s))
"""
return [(i, j) for i in range(self.rows)
for j in range(self.cols) if (i, j) not in self.walls]
def getTransitionStatesAndProbs(self, state, action):
"""
get all (next state, p(s' | s, a)), in terms of stochastic action
:return: list of (next_state, probability to the next state given current state and action)
"""
if state in self.terminals:
# if the state is terminal state, the probability of game over is 1
return [(GridWorldEnv.GAMEOVER, 1.0)]
result = []
for turn in self.turns: # loop over all turns(west, north, east)
# turn west, north, or east of the "planned" action for the "real" action
# -1, 0, 1, or 2 % 4 to get the "real" tuple of direction(action), e.g.:
# planned: EAST, index 1 => turn is WEST(of EAST), index -1 => 1 + -1 = 0 => mod 4 => 0: real action NORTH
# => turn is NORTH(of EAST), index 0 => 1 + 0 = 1 => mod 4 => 1: real action EAST
direction = GridWorldEnv.ACTIONS[(GridWorldEnv.index[action] + turn) % len(GridWorldEnv.ACTIONS)]
row = state[0] + direction[0] # x coordinate of next state
col = state[1] + direction[1] # y coordinate of next state
next_state = (row if 0 <= row < self.rows else state[0],
col if 0 <= col < self.cols else state[1]) # possible next state considered wall(s)
if next_state in self.walls: # stay if is wall
next_state = state
prob = self.turns[turn]
result.append((next_state, prob))
return result
def getReward(self, state, action, nextState):
"""
r(s, a, s')
"""
if state in self.terminals:
return self.terminals[state] # get reward(penalty) for terminal states
else:
return self.alive_reward # alive exploration rewards
@staticmethod
def isTerminal(next_state):
"""
check if next state is terminal state, and by convenience, the next state of terminals is (-1, -1)
"""
return next_state == GridWorldEnv.GAMEOVER
def getLegalActions(self, state):
"""
get all possible actions, if state the terminal, by convenience return (INF, INF)
"""
if state in self.terminals:
return [GridWorldEnv.EXIT]
else:
return GridWorldEnv.ACTIONS
def to_2d_array(self, in_list, add=None):
"""
input list to 2D array(matrix) based on rows and columns
"""
mat = []
k = False
for i in range(self.rows):
temp = []
for j in range(self.cols):
if add is not None:
if (i, j) in self.walls:
temp.append(add)
k = True
continue
if k:
temp.append(in_list[i * self.cols + j - 1])
else:
temp.append(in_list[i * self.cols + j])
mat.append(temp)
return mat
def printValues(self, values):
"""
visualize values in a table
"""
fig, ax = plt.subplots()
ax.set_axis_off()
tb = Table(ax, bbox=[0, 0, 1, 1])
values = list(values.values())
values = np.round(np.array(self.to_2d_array(values, add=0)), decimals=2)
width, height = 1.0 / self.rows, 1.0 / self.cols
# Add cells
for (i, j), val in np.ndenumerate(values):
tb.add_cell(i, j, width, height, text=val,
loc='center', facecolor='white')
# Row and column labels...
n = max(self.rows, self.cols)
for i in range(n):
if i < self.rows:
tb.add_cell(i, -1, width, height, text=self.rows-i, loc='right',
edgecolor='none', facecolor='none')
if i < self.cols:
tb.add_cell(self.rows, i, width, height / 2, text=i+1, loc='center',
edgecolor='none', facecolor='none')
tb.set_fontsize(13)
ax.add_table(tb)
plt.plot()
def printQValues(self, q_values):
fig, ax = plt.subplots()
ax.set_axis_off()
tb = Table(ax, bbox=[0, 0, 1, 1])
width, height = 1.0 / self.rows, 1.0 / self.cols
qs = []
for i in range(self.rows):
for j in range(self.cols):
q = ''
if (i, j) in self.walls or (i, j) in list(self.terminals.keys()):
q += " \n"
else:
q += " %.2f \n" % (q_values[(i, j), GridWorldEnv.NORTH])
if (i, j) in self.walls:
q += " \n"
elif (i, j) in self.terminals:
q += " %.2f \n" % q_values[(i, j), GridWorldEnv.EXIT]
else:
q += "%.2f %.2f\n" % (q_values[(i, j), GridWorldEnv.WEST], q_values[(i, j), GridWorldEnv.EAST])
if (i, j) in self.walls or (i, j) in list(self.terminals.keys()):
q += " "
else:
q += " %.2f " % (q_values[(i, j), GridWorldEnv.SOUTH])
qs.append(q)
qs = self.to_2d_array(qs)
qs = np.array(qs)
for (i, j), q in np.ndenumerate(qs):
tb.add_cell(i, j, width, height, text=q,
loc='center', facecolor='white')
n = max(self.rows, self.cols)
for i in range(n):
if i < self.rows:
tb.add_cell(i, -1, width, height, text=self.rows - i, loc='right',
edgecolor='none', facecolor='none')
if i < self.cols:
tb.add_cell(self.rows, i, width, height / 2, text=i + 1, loc='center',
edgecolor='none', facecolor='none')
tb.set_fontsize(15)
ax.add_table(tb)
plt.plot()
def printPolicy(self, policy):
action_map = {0: '↑', 1: '→',
2: '↓', 3: '←',
-1: ' '}
policy = list(policy.values())
policy = self.to_2d_array(policy, add=-1)
policy = np.array(policy, dtype=object)
fig, ax = plt.subplots()
ax.set_axis_off()
tb = Table(ax, bbox=[0, 0, 1, 1])
width, height = 1.0 / self.rows, 1.0 / self.cols
for (i, j), action in np.ndenumerate(policy):
if (i, j) in self.walls:
tb.add_cell(i, j, width, height, text='',
loc='center', facecolor='gray')
elif (i, j) == list(self.terminals.keys())[0]:
tb.add_cell(i, j, width, height, text='+1',
loc='center', facecolor='blue')
elif (i, j) == list(self.terminals.keys())[1]:
tb.add_cell(i, j, width, height, text='-1',
loc='center', facecolor='red')
else:
tb.add_cell(i, j, width, height, text=action_map[action],
loc='center', facecolor='white')
n = max(self.rows, self.cols)
for i in range(n):
if i < self.rows:
tb.add_cell(i, -1, width, height, text=self.rows - i, loc='right',
edgecolor='none', facecolor='none')
if i < self.cols:
tb.add_cell(self.rows, i, width, height / 2, text=i + 1, loc='center',
edgecolor='none', facecolor='none')
tb.set_fontsize(13)
ax.add_table(tb)
plt.plot()
"""
--------------------------------------------------------------------------------------
Bellman Equation:
v(s) = Σ_{a} π(a | s) Σ_{s', r} p(s', r | s, a) * [r + γ * v(s')]
Bellman Optimality Equation:
v*(s) = max_{a} { Σ p(s', r | s, a) * [r + γ * v(s')] }
= max q_{π*} (s, a) = max q(s, a), as π(a | s) is unchanged in this MDP problem
@author: Charles Zhang
@date Mar 28, 2021
--------------------------------------------------------------------------------------
"""
from collections import defaultdict
# MDP Value Iteration with Bellman update
class ValueIteration:
"""
Class to Find Optimal Value Functions
"""
def valueIteration(self, GridWorld, discount=0.9, iterations=100):
"""
Implement the value iteration algorithm by the optimal value function derived by Bellman equation
v*(s) = max q(s, a)
:param GridWorld: gridworld environment
:param discount: discount gamma
:param iterations: iteration times
:return dictionary of values of all states
"""
values = defaultdict(lambda: 0) # initialize values with all 0 of states
for i in range(iterations): # or while TRUE:
vnext = defaultdict(lambda: 0) # initialize values for each iteration with all 0 of states
for state in GridWorld.getStates(): # loop over all possible state(all states except wall(s))
if not GridWorld.isTerminal(state): # check if the state is terminal
maximum = float("-inf")
for action in GridWorld.getLegalActions(state): # loop over all possible actions
q_value = self.get_q_from_v(GridWorld, state, action, values, discount)
maximum = max(maximum, q_value) # update the max q value among actions of current state
vnext[state] = maximum # optimal v*(s) = max q(s, a)
values = vnext # update the new value table
# if while TURE above, here could compare the difference between
# values and vnext to see if converges, and end the loop
return values
@staticmethod
def get_q_from_v(GridWorld, state, action, values, discount=0.9):
"""
get q(s, a) from values v(s) and action a by
Bellman Equation: q(s, a) = Σ p(s', r | s, a) * [r + γ * v(s')]
:param GridWorld: gridworld environment
:param state: current state s
:param action: current selected action a
:param values: current values table
:param discount: discount gamma
:return: float q(s, a)
"""
q_val = 0
# implement Bellman equation: q(s, a) = Σ p(s', r | s, a) * [r + γ * v(s')]
for next_state, prob in GridWorld.getTransitionStatesAndProbs(state, action):
q_val += prob * (GridWorld.getReward(state, action, next_state) + discount * values[next_state])
return q_val
def getQValues(self, GridWorld, values, discount=0.9):
"""
Get q values by Values
:return dictionary of q values of all states
"""
q_values = {}
for state in GridWorld.getStates():
if not GridWorld.isTerminal(state):
for action in GridWorld.getLegalActions(state):
q_values[state, action] = self.get_q_from_v(GridWorld, state, action, values, discount)
return q_values
def getPolicy(self, GridWorld, values, discount=0.9):
"""
get policy by values
π*(s) ≈ π(s) = argmax_a Σ p(s', r | s, a) * [r + γ * v(s')] = argmax_a q(s, a)
:return dictionary of optimal actions of all states
"""
policy = {}
for state in GridWorld.getStates():
if not GridWorld.isTerminal(state):
maximum = -float("inf")
best_action = None
# Choose action for the policy based no the max q values among actions of state s
for action in GridWorld.getLegalActions(state):
q_value = self.get_q_from_v(GridWorld, state, action, values, discount)
if q_value > maximum:
maximum = q_value
best_action = action
best_action = GridWorld.index[best_action]
policy[state] = best_action
return policy
No Alive Reward (discount reward $\gamma = 0.9$)¶
gamma = 0.9
alive_reward = 0.0
print("GridWorld Value Iteration with alive reward = %.2f, discount gamma = %.2f\n" % (alive_reward, gamma))
terminals = {(0, 3): 1, (1, 3): -1}
gridworld0 = GridWorldEnv(shape=(3, 4), prob=0.8, walls=[(1, 1)], terminals=terminals, alive_reward=0.0)
vi = ValueIteration()
values = vi.valueIteration(GridWorld=gridworld0, discount=gamma)
gridworld0.printValues(values)
q_values = vi.getQValues(GridWorld=gridworld0, values=values, discount=gamma)
gridworld0.printQValues(q_values)
policy = vi.getPolicy(GridWorld=gridworld0, values=values, discount=gamma)
gridworld0.printPolicy(policy)
With Alive Reward ($\gamma = 1$)¶
reward = -0.01
print("Grid world Value Iteration with alive rewards = %.2f\n" % reward)
gridworld001 = GridWorldEnv((3, 4), 0.8, [(1, 1)], terminals, reward)
values = vi.valueIteration(gridworld001, 1, 100)
gridworld001.printValues(values)
# q_values = vi.getQValues(gridworld001, values, 1)
# gridworld001.printQValues(q_values)
policy = vi.getPolicy(gridworld001, values, 1)
gridworld001.printPolicy(policy)
reward = -0.03
print("Grid world Value Iteration with alive rewards = %.2f\n" % reward)
gridworld003 = GridWorldEnv((3, 4), 0.8, [(1, 1)], terminals, reward)
values = vi.valueIteration(gridworld003, 1, 100)
gridworld003.printValues(values)
# q_values = vi.getQValues(gridworld003, values, 1)
# gridworld003.printQValues(q_values)
policy = vi.getPolicy(gridworld003, values, 1)
gridworld003.printPolicy(policy)
reward = -0.4
print("Grid World with additive rewards = %.2f\n" % reward)
gridworld04 = GridWorldEnv((3, 4), 0.8, [(1, 1)], terminals, reward)
values = vi.valueIteration(gridworld04, 1, 100)
gridworld04.printValues(values)
# q_values = vi.getQValues(gridworld04, values, 1)
# gridworld04.printQValues(q_values)
policy = vi.getPolicy(gridworld04, values, 1)
gridworld04.printPolicy(policy)
reward = -2
print("Grid World with additive rewards = %.2f\n" % reward)
gridworld2 = GridWorldEnv((3, 4), 0.8, [(1, 1)], terminals, reward)
values = vi.valueIteration(gridworld2, 1, 100)
gridworld2.printValues(values)
# q_values = vi.getQValues(gridworld2, values, 1)
# gridworld2.printQValues(q_values)
policy = vi.getPolicy(gridworld2, values, 1)
gridworld2.printPolicy(policy)
Implementation for Example 3.8: GridWorld¶
Example 3.8: Gridworld Figure below uses a rectangular grid to illustrate value functions for a simple finite MDP. The cells of the grid correspond to the states of the environment. At each cell, four actions are possible: north, south, east, and west, which deterministically cause the agent to move one cell in the respective direction on the grid. Actions that would take the agent off the grid leave its location unchanged, but also result in a reward of -1 . Other actions result in a reward of $0,$ except those that move the agent out of the special states $\mathrm{A}$ and $\mathrm{B}$. From state $\mathrm{A},$ all four actions yield a reward of +10 and take the agent to $\mathrm{A}^{\prime}$. From state $\mathrm{B},$ all actions yield a reward of +5 and take the agent to $\mathrm{B}^{\prime}$. Suppose the agent selects all four actions with equal probability in all states.

import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.table import Table
WORLD_SIZE = 5
A_POS = [0, 1]
A_PRIME_POS = [4, 1]
B_POS = [0, 3]
B_PRIME_POS = [2, 3]
DISCOUNT = 0.9
# left, up, right, down
ACTIONS = [np.array([0, -1]),
np.array([-1, 0]),
np.array([0, 1]),
np.array([1, 0])]
ACTIONS_FIGS = ['←', '↑', '→', '↓']
ACTION_PROB = 0.25
def step(state, action):
if state == A_POS:
return A_PRIME_POS, 10
if state == B_POS:
return B_PRIME_POS, 5
next_state = (np.array(state) + action).tolist()
x, y = next_state
if x < 0 or x >= WORLD_SIZE or y < 0 or y >= WORLD_SIZE:
reward = -1.0
next_state = state
else:
reward = 0
return next_state, reward
def draw_image(image):
fig, ax = plt.subplots()
ax.set_axis_off()
tb = Table(ax, bbox=[0, 0, 1, 1])
nrows, ncols = image.shape
width, height = 1.0 / ncols, 1.0 / nrows
# Add cells
for (i, j), val in np.ndenumerate(image):
# add state labels
if [i, j] == A_POS:
val = str(val) + " (A)"
if [i, j] == A_PRIME_POS:
val = str(val) + " (A')"
if [i, j] == B_POS:
val = str(val) + " (B)"
if [i, j] == B_PRIME_POS:
val = str(val) + " (B')"
tb.add_cell(i, j, width, height, text=val,
loc='center', facecolor='white')
# Row and column labels...
for i in range(len(image)):
tb.add_cell(i, -1, width, height, text=i + 1, loc='right',
edgecolor='none', facecolor='none')
tb.add_cell(-1, i, width, height / 2, text=i + 1, loc='center',
edgecolor='none', facecolor='none')
ax.add_table(tb)
def draw_policy(optimal_values):
fig, ax = plt.subplots()
ax.set_axis_off()
tb = Table(ax, bbox=[0, 0, 1, 1])
nrows, ncols = optimal_values.shape
width, height = 1.0 / ncols, 1.0 / nrows
# Add cells
for (i, j), val in np.ndenumerate(optimal_values):
next_vals = []
for action in ACTIONS:
next_state, _ = step([i, j], action)
next_vals.append(optimal_values[next_state[0], next_state[1]])
best_actions = np.where(next_vals == np.max(next_vals))[0]
val = ''
for ba in best_actions:
val += ACTIONS_FIGS[ba]
# add state labels
if [i, j] == A_POS:
val = str(val) + " (A)"
if [i, j] == A_PRIME_POS:
val = str(val) + " (A')"
if [i, j] == B_POS:
val = str(val) + " (B)"
if [i, j] == B_PRIME_POS:
val = str(val) + " (B')"
tb.add_cell(i, j, width, height, text=val,
loc='center', facecolor='white')
# Row and column labels...
for i in range(len(optimal_values)):
tb.add_cell(i, -1, width, height, text=i + 1, loc='right',
edgecolor='none', facecolor='none')
tb.add_cell(-1, i, width, height / 2, text=i + 1, loc='center',
edgecolor='none', facecolor='none')
ax.add_table(tb)
def figure_3_5_b():
value = np.zeros((WORLD_SIZE, WORLD_SIZE))
while True:
# keep iteration until convergence
new_value = np.zeros_like(value)
for i in range(WORLD_SIZE):
for j in range(WORLD_SIZE):
for action in ACTIONS:
(next_i, next_j), reward = step([i, j], action)
# bellman equation
new_value[i, j] += ACTION_PROB * (reward + DISCOUNT * value[next_i, next_j])
if np.sum(np.abs(value - new_value)) < 1e-4:
draw_image(np.round(new_value, decimals=2))
plt.plot()
break
value = new_value
figure_3_5_b()
def figure_3_5_b_linear_system():
"""
Here we solve the linear system of equations to find the exact solution.
We do this by filling the coefficients for each of the states with their respective right side constant.
"""
A = -1 * np.eye(WORLD_SIZE * WORLD_SIZE)
b = np.zeros(WORLD_SIZE * WORLD_SIZE)
for i in range(WORLD_SIZE):
for j in range(WORLD_SIZE):
s = [i, j] # current state
index_s = np.ravel_multi_index(s, (WORLD_SIZE, WORLD_SIZE))
for a in ACTIONS:
s_, r = step(s, a)
index_s_ = np.ravel_multi_index(s_, (WORLD_SIZE, WORLD_SIZE))
A[index_s, index_s_] += ACTION_PROB * DISCOUNT
b[index_s] -= ACTION_PROB * r
x = np.linalg.solve(A, b)
draw_image(np.round(x.reshape(WORLD_SIZE, WORLD_SIZE), decimals=2))
plt.plot()
figure_3_5_b_linear_system()
def figure_3_8():
value = np.zeros((WORLD_SIZE, WORLD_SIZE))
while True:
# keep iteration until convergence
new_value = np.zeros_like(value)
for i in range(WORLD_SIZE):
for j in range(WORLD_SIZE):
values = []
for action in ACTIONS:
(next_i, next_j), reward = step([i, j], action)
# value iteration
values.append(reward + DISCOUNT * value[next_i, next_j])
new_value[i, j] = np.max(values)
if np.sum(np.abs(new_value - value)) < 1e-4:
draw_image(np.round(new_value, decimals=2))
plt.plot()
draw_policy(new_value)
break
value = new_value
figure_3_8()
Reference:
[1] Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction. MIT press, 2018.
[3] https://github.com/ShangtongZhang/reinforcement-learning-an-introduction
