Policy Evaluation

Idea: \(\displaystyle \lim_{k\rightarrow\infty} v_k = v_\pi\). From the Bellman equation for value function \(v(s)\) in last chapter, there are \(n\) linear equations with \(n\) states, \(v_{k+1} = \boldsymbol{C}\cdot v_k + \boldsymbol{b}\) where \(\boldsymbol{C}\text{ is } n\times n \) matrix of coefficients of \(v_k\) and \( \boldsymbol{b} \text{ is a } n \text{ vector for constants in Bellman equation}\). Therefore, it could be solved using Jacobi, or Gauss-Seidel iterate method, or other numerical techiniques. And this iteration would coverage if and only if \(\displaystyle\lim_{k\rightarrow\infty} C^k = \text{zero matrix }\boldsymbol{O}\). To prove, let
\( \boldsymbol{C}=\left[\begin{array}{cccc} c_{11} & c_{12} & \cdots & c_{1 n} \\ c_{21} & c_{22} & \cdots & c_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ c_{n 1} & c_{n 2} & \cdots & c_{n n} \end{array}\right], \text{ and } \boldsymbol{b}=\left[\begin{array}{c} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \end{array}\right] \)
where from the bellman equation,
\( \begin{aligned} c_{i j} &=\sum_{a} \pi\left(a | s_{i}\right) \sum_{r} p\left(s_{j}, r | s_{i}, a\right) \gamma \\ & \leq \sum_{a} \pi\left(a | s_{i}\right) \sum_{s_{j}, r} p\left(s_{j}, r | s_{i}, a\right) \gamma\\ &= \gamma\\ b_{i} &=\sum_{a} \pi\left(a | s_{i}\right) \sum_{r} p\left(r | s_{i}, a\right) r \end{aligned} \)
Therefore, when \(\gamma \in [0,1)\),
\(\lim _{k \rightarrow \infty} \boldsymbol{C}^{k} \leq \lim _{k \rightarrow \infty}\left[\begin{array}{cccc} \gamma & \gamma & \cdots & \gamma \\ \gamma & \gamma & \cdots & \gamma \\ \vdots & \vdots & \ddots & \vdots \\ \gamma & \gamma & \cdots & \gamma \end{array}\right]^{k}=\boldsymbol{O}\)
The DP algorith:

Policy Improvement

Idea: using greedy \(\pi'(s), \pi(s)\in\mathcal{A}\), \(q_\pi (s,\pi'(s)) \geq v_\pi(s) \Rightarrow v_{\pi'}(s)\geq v_\pi(s)\)
Proof:
\(\begin{aligned} q_{\pi}(s, a) & \doteq \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s, A_{t}=a\right]=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma v_{\pi}(s) \mid s, a\right] \\ v_{\pi}(s) & \leq q_{\pi}\left(s, \pi^{\prime}(s)\right) \\ &=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=\pi^{\prime}(s)\right] \\ &=\mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s\right] \\ & \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma q_{\pi}\left(S_{t+1}, \pi^{\prime}\left(S_{t+1}\right)\right) \mid S_{t}=s\right] \\ &=\mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma \mathbb{E}_{\pi^{\prime}}\left[R_{t+2}+\gamma v_{\pi}\left(S_{t+2}\right)\right] \mid S_{t}=s\right] \\ &=\mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} v_{\pi}\left(S_{t+2}\right) \mid S_{t}=s\right] \\ & \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\gamma^{3} v_{\pi}\left(S_{t+3}\right) \mid S_{t}=s\right] \\ \vdots & \\ & \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\gamma^{3} R_{t+4}+\cdots \mid S_{t}=s\right] \\ &=\mathbb{E}_{\pi^{\prime}}\left[G_{t} \mid S_{t}=s\right] \\ &=v_{\pi^{\prime}}(s) \end{aligned}\)
And the equation for updating new greedy policy \(\pi'\): \[ \begin{aligned} \pi^{\prime}(s) & \doteq \underset{a}{\arg \max } q_{\pi}(s, a) \\ &=\underset{a}{\arg \max } \mathbb{E}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] \\ &=\underset{a}{\arg \max } \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right] \end{aligned} \]

Policy Iteration

Idea: \(\pi_0 \xrightarrow{E} v_{\pi_0} \xrightarrow{I} \pi_1 \xrightarrow{E} v_{\pi_1} \xrightarrow{I} \pi_2 \xrightarrow{E} ... \xrightarrow{I} \pi_* \xrightarrow{E} v_* \), where \(\xrightarrow{E}\) is policy evaluation and \(\xrightarrow{I}\) is policy improvement.
The DP algorithm below illustrates this iteration directly:

Value Iteration

Idea: update operation that combines the policy improvement and truncated policy evaluation steps:
\(\begin{aligned} v_{k+1}(s) & \doteq \max _{a} \mathbb{E}\left[R_{t+1}+\gamma v_{k}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] \\ &=\max _{a} \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{k}\left(s^{\prime}\right)\right], \text{ }\forall s\in\mathcal{S} \end{aligned}\)
As for arbitrary \(v_0\), \(\{v_k\}\) is shown to be guaranteed to converge to \(v_*\) by the bellman equation illustrated last chapter. The DP algorithm below follows this update:

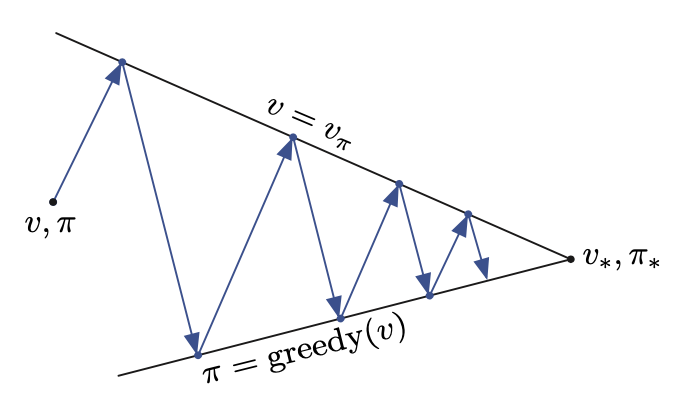
Generalized Policy Iteration (GPI)

Important model in reinforcement learnig. e.g. policy-evaluation and policy-improvement processes.

The process and convergence is clearly illustrated in the figure below:

</div> </div> </div>

Implementation of Stochastic GridWorld

This also shown in my MDP note.

Using Bellman Optimality Equation: $v*(s) = \max_a \{\sum_{s',r} p(s', r\mid s, a)\cdot [r + \gamma \cdot v(s')]\} = \max q_{\pi*}(s, a)$

The explanations, use of equations, and details for implementation are all detailed commented in the code below.

"""
--------------------------
Environment

 c   0    1    2    3
r  - - - - - - - - - -
0 |    |    |    | +1 |
   - - - - - - - - - -
1 |    |WALL|    | -1 |
   - - - - - - - - - -
2 |    |    |    |    |
   - - - - - - - - - -

For Visualization:

   - - - - - - - - - -
3 |    |    |    | +1 |
   - - - - - - - - - -
2 |    |WALL|    | -1 |
   - - - - - - - - - -
1 |    |    |    |    |
r  - - - - - - - - - -
  c  1    2    3    4

@author: Charles Zhang
@date Mar 28, 2021
---------------------------
"""
import numpy as np
from matplotlib.table import Table
import matplotlib.pyplot as plt


# Grid Environment for MDP Value Iteration
class GridWorldEnv:

    EXIT  = (float("inf"), float("inf"))
    # actions
    NORTH = (-1, 0)
    EAST  = (0, 1)
    SOUTH = (1, 0)
    WEST  = (0, -1)
    ACTIONS = [NORTH, EAST, SOUTH, WEST]
    index = {NORTH: 0, EAST: 1, SOUTH: 2, WEST: 3, EXIT: -1}
    GAMEOVER = (-1, -1)     # by convenience, the next state of terminals is (-1, -1)

    def __init__(self, shape, prob, walls, terminals, alive_reward=0.0):
        """
        :param shape: shape of gridworld: (row, col)
        :param prob: probability to go north(for stochastic move)
        :param walls: list of walls: [(1, 1)] if only one wall at (1, 1)
        :param terminals: dictionary of goal and death terminal states with reward
               {(0, 3): +1, (1, 3): -1} in this problem
        :param alive_reward: alive reward
        """
        self.rows, self.cols = shape
        p_not_north = (1 - prob) / 2
        self.turns = {-1: p_not_north, 0: prob, 1: p_not_north}    # turn west, north, or east
        self.walls = set(walls)
        self.terminals = terminals
        self.alive_reward = alive_reward

    def getStates(self):
        """
        All available states(all states except wall(s))
        """
        return [(i, j) for i in range(self.rows)
                for j in range(self.cols) if (i, j) not in self.walls]

    def getTransitionStatesAndProbs(self, state, action):
        """
        get all (next state, p(s' | s, a)), in terms of stochastic action
        :return: list of (next_state, probability to the next state given current state and action)
        """
        if state in self.terminals:
            # if the state is terminal state, the probability of game over is 1
            return [(GridWorldEnv.GAMEOVER, 1.0)]
        result = []
        for turn in self.turns:     # loop over all turns(west, north, east)
            # turn west, north, or east of the "planned" action for the "real" action
            # -1, 0, 1, or 2 % 4 to get the "real" tuple of direction(action), e.g.:
            # planned: EAST, index 1 => turn is WEST(of EAST), index -1 => 1 + -1 = 0 => mod 4 => 0: real action NORTH
            #                        => turn is NORTH(of EAST), index 0 => 1 + 0 = 1 => mod 4 => 1: real action EAST
            direction = GridWorldEnv.ACTIONS[(GridWorldEnv.index[action] + turn) % len(GridWorldEnv.ACTIONS)]
            row = state[0] + direction[0]      # x coordinate of next state
            col = state[1] + direction[1]      # y coordinate of next state
            next_state = (row if 0 <= row < self.rows else state[0],
                          col if 0 <= col < self.cols else state[1])       # possible next state considered wall(s)
            if next_state in self.walls:    # stay if is wall
                next_state = state
            prob = self.turns[turn]
            result.append((next_state, prob))
        return result

    def getReward(self, state, action, nextState):
        """
        r(s, a, s')
        """
        if state in self.terminals:
            return self.terminals[state]    # get reward(penalty) for terminal states
        else:
            return self.alive_reward        # alive exploration rewards

    @staticmethod
    def isTerminal(next_state):
        """
        check if next state is terminal state, and by convenience, the next state of terminals is (-1, -1)
        """
        return next_state == GridWorldEnv.GAMEOVER

    def getLegalActions(self, state):
        """
        get all possible actions, if state the terminal, by convenience return (INF, INF)
        """
        if state in self.terminals:
            return [GridWorldEnv.EXIT]
        else:
            return GridWorldEnv.ACTIONS

    def to_2d_array(self, in_list, add=None):
        """
        input list to 2D array(matrix) based on rows and columns
        """
        mat = []
        k = False
        for i in range(self.rows):
            temp = []
            for j in range(self.cols):
                if add is not None:
                    if (i, j) in self.walls:
                        temp.append(add)
                        k = True
                        continue
                if k:
                    temp.append(in_list[i * self.cols + j - 1])
                else:
                    temp.append(in_list[i * self.cols + j])
            mat.append(temp)
        return mat

    def printValues(self, values):
        """
        visualize values in a table
        """
        fig, ax = plt.subplots()
        ax.set_axis_off()
        tb = Table(ax, bbox=[0, 0, 1, 1])
        values = list(values.values())
        values = np.round(np.array(self.to_2d_array(values, add=0)), decimals=2)
        width, height = 1.0 / self.rows, 1.0 / self.cols
        # Add cells
        for (i, j), val in np.ndenumerate(values):
            tb.add_cell(i, j, width, height, text=val,
                        loc='center', facecolor='white')
        # Row and column labels...
        n = max(self.rows, self.cols)
        for i in range(n):
            if i < self.rows:
                tb.add_cell(i, -1, width, height, text=self.rows-i, loc='right',
                            edgecolor='none', facecolor='none')
            if i < self.cols:
                tb.add_cell(self.rows, i, width, height / 2, text=i+1, loc='center',
                            edgecolor='none', facecolor='none')
        tb.set_fontsize(13)
        ax.add_table(tb)
        plt.plot()

    def printQValues(self, q_values):
        fig, ax = plt.subplots()
        ax.set_axis_off()
        tb = Table(ax, bbox=[0, 0, 1, 1])
        width, height = 1.0 / self.rows, 1.0 / self.cols
        qs = []
        for i in range(self.rows):
            for j in range(self.cols):
                q = ''
                if (i, j) in self.walls or (i, j) in list(self.terminals.keys()):
                    q += "           \n"
                else:
                    q += "   %.2f   \n" % (q_values[(i, j), GridWorldEnv.NORTH])
                if (i, j) in self.walls:
                    q += "           \n"
                elif (i, j) in self.terminals:
                    q += "   %.2f   \n" % q_values[(i, j), GridWorldEnv.EXIT]
                else:
                    q += "%.2f    %.2f\n" % (q_values[(i, j), GridWorldEnv.WEST], q_values[(i, j), GridWorldEnv.EAST])
                if (i, j) in self.walls or (i, j) in list(self.terminals.keys()):
                    q += "           "
                else:
                    q += "   %.2f   " % (q_values[(i, j), GridWorldEnv.SOUTH])
                qs.append(q)
        qs = self.to_2d_array(qs)
        qs = np.array(qs)
        for (i, j), q in np.ndenumerate(qs):
            tb.add_cell(i, j, width, height, text=q,
                        loc='center', facecolor='white')
        n = max(self.rows, self.cols)
        for i in range(n):
            if i < self.rows:
                tb.add_cell(i, -1, width, height, text=self.rows - i, loc='right',
                            edgecolor='none', facecolor='none')
            if i < self.cols:
                tb.add_cell(self.rows, i, width, height / 2, text=i + 1, loc='center',
                            edgecolor='none', facecolor='none')
        tb.set_fontsize(15)
        ax.add_table(tb)
        plt.plot()

    def printPolicy(self, policy):
        action_map = {0: '↑', 1: '→',
                  2: '↓', 3: '←',
                  -1: ' '}
        policy = list(policy.values())
        policy = self.to_2d_array(policy, add=-1)
        policy = np.array(policy, dtype=object)
        fig, ax = plt.subplots()
        ax.set_axis_off()
        tb = Table(ax, bbox=[0, 0, 1, 1])
        width, height = 1.0 / self.rows, 1.0 / self.cols
        for (i, j), action in np.ndenumerate(policy):
            if (i, j) in self.walls:
                tb.add_cell(i, j, width, height, text='',
                            loc='center', facecolor='gray')
            elif (i, j) == list(self.terminals.keys())[0]:
                 tb.add_cell(i, j, width, height, text='+1',
                            loc='center', facecolor='blue')
            elif (i, j) == list(self.terminals.keys())[1]:
                tb.add_cell(i, j, width, height, text='-1',
                            loc='center', facecolor='red')
            else:
                tb.add_cell(i, j, width, height, text=action_map[action],
                            loc='center', facecolor='white')

        n = max(self.rows, self.cols)
        for i in range(n):
            if i < self.rows:
                tb.add_cell(i, -1, width, height, text=self.rows - i, loc='right',
                            edgecolor='none', facecolor='none')
            if i < self.cols:
                tb.add_cell(self.rows, i, width, height / 2, text=i + 1, loc='center',
                            edgecolor='none', facecolor='none')
        tb.set_fontsize(13)
        ax.add_table(tb)
        plt.plot()

        
"""
--------------------------------------------------------------------------------------
Bellman Equation:
v(s) = Σ_{a} π(a | s) Σ_{s', r} p(s', r | s, a) * [r + γ * v(s')]
Bellman Optimality Equation:
v*(s) = max_{a} { Σ p(s', r | s, a) * [r + γ * v(s')] }
      = max q_{π*} (s, a) = max q(s, a), as π(a | s) is unchanged in this MDP problem
@author: Charles Zhang
@date Mar 28, 2021
--------------------------------------------------------------------------------------
"""
from collections import defaultdict


# MDP Value Iteration with Bellman update
class ValueIteration:
    """
    Class to Find Optimal Value Functions
    """

    def valueIteration(self, GridWorld, discount=0.9, iterations=100):
        """
        Implement the value iteration algorithm by the optimal value function derived by Bellman equation
        v*(s) = max q(s, a)
        :param GridWorld: gridworld environment
        :param discount: discount gamma
        :param iterations: iteration times
        :return dictionary of values of all states
        """
        values = defaultdict(lambda: 0)     # initialize values with all 0 of states
        for i in range(iterations):         # or while TRUE:
            vnext = defaultdict(lambda: 0)           # initialize values for each iteration with all 0 of states
            for state in GridWorld.getStates():      # loop over all possible state(all states except wall(s))
                if not GridWorld.isTerminal(state):  # check if the state is terminal
                    maximum = float("-inf")
                    for action in GridWorld.getLegalActions(state):     # loop over all possible actions
                        q_value = self.get_q_from_v(GridWorld, state, action, values, discount)
                        maximum = max(maximum, q_value)     # update the max q value among actions of current state
                    vnext[state] = maximum      # optimal v*(s) = max q(s, a)
            values = vnext      # update the new value table
            # if while TURE above, here could compare the difference between
            # values and vnext to see if converges, and end the loop
        return values

    @staticmethod
    def get_q_from_v(GridWorld, state, action, values, discount=0.9):
        """
        get q(s, a) from values v(s) and action a by
        Bellman Equation: q(s, a) = Σ p(s', r | s, a) * [r + γ * v(s')]
        :param GridWorld: gridworld environment
        :param state: current state s
        :param action: current selected action a
        :param values: current values table
        :param discount: discount gamma
        :return: float q(s, a)
        """
        q_val = 0
        # implement Bellman equation: q(s, a) = Σ p(s', r | s, a) * [r + γ * v(s')]
        for next_state, prob in GridWorld.getTransitionStatesAndProbs(state, action):
            q_val += prob * (GridWorld.getReward(state, action, next_state) + discount * values[next_state])
        return q_val

    def getQValues(self, GridWorld, values, discount=0.9):
        """
        Get q values by Values
        :return dictionary of q values of all states
        """
        q_values = {}
        for state in GridWorld.getStates():
            if not GridWorld.isTerminal(state):
                for action in GridWorld.getLegalActions(state):
                    q_values[state, action] = self.get_q_from_v(GridWorld, state, action, values, discount)
        return q_values

    def getPolicy(self, GridWorld, values, discount=0.9):
        """
        get policy by values
        π*(s) ≈ π(s) = argmax_a Σ p(s', r | s, a) * [r + γ * v(s')] = argmax_a q(s, a)
        :return dictionary of optimal actions of all states
        """
        policy = {}
        for state in GridWorld.getStates():
            if not GridWorld.isTerminal(state):
                maximum = -float("inf")
                best_action = None
                # Choose action for the policy based no the max q values among actions of state s
                for action in GridWorld.getLegalActions(state):
                    q_value = self.get_q_from_v(GridWorld, state, action, values, discount)
                    if q_value > maximum:
                        maximum = q_value
                        best_action = action
                best_action = GridWorld.index[best_action]
                policy[state] = best_action
        return policy

No Alive Reward (discount reward $\gamma = 0.9$)

gamma = 0.9
alive_reward = 0.0
print("GridWorld Value Iteration with alive reward = %.2f, discount gamma  = %.2f\n" % (alive_reward, gamma))
terminals = {(0, 3): 1, (1, 3): -1}
gridworld0 = GridWorldEnv(shape=(3, 4), prob=0.8, walls=[(1, 1)], terminals=terminals, alive_reward=0.0)
vi = ValueIteration()
values = vi.valueIteration(GridWorld=gridworld0, discount=gamma)
gridworld0.printValues(values)

GridWorld Value Iteration with alive reward = 0.00, discount gamma  = 0.90

q_values = vi.getQValues(GridWorld=gridworld0, values=values, discount=gamma)
gridworld0.printQValues(q_values)

policy = vi.getPolicy(GridWorld=gridworld0, values=values, discount=gamma)
gridworld0.printPolicy(policy)

With Alive Reward ($\gamma = 1$)

reward = -0.01
print("Grid world Value Iteration with alive rewards = %.2f\n" % reward)
gridworld001 = GridWorldEnv((3, 4), 0.8, [(1, 1)], terminals, reward)
values = vi.valueIteration(gridworld001, 1, 100)
gridworld001.printValues(values)
# q_values = vi.getQValues(gridworld001, values, 1)
# gridworld001.printQValues(q_values)

Grid world Value Iteration with alive rewards = -0.01

policy = vi.getPolicy(gridworld001, values, 1)
gridworld001.printPolicy(policy)

reward = -0.03
print("Grid world Value Iteration with alive rewards = %.2f\n" % reward)
gridworld003 = GridWorldEnv((3, 4), 0.8, [(1, 1)], terminals, reward)
values = vi.valueIteration(gridworld003, 1, 100)
gridworld003.printValues(values)
# q_values = vi.getQValues(gridworld003, values, 1)
# gridworld003.printQValues(q_values)

Grid world Value Iteration with alive rewards = -0.03

policy = vi.getPolicy(gridworld003, values, 1)
gridworld003.printPolicy(policy)

reward = -0.4
print("Grid World with additive rewards = %.2f\n" % reward)
gridworld04 = GridWorldEnv((3, 4), 0.8, [(1, 1)], terminals, reward)
values = vi.valueIteration(gridworld04, 1, 100)
gridworld04.printValues(values)
# q_values = vi.getQValues(gridworld04, values, 1)
# gridworld04.printQValues(q_values)

Grid World with additive rewards = -0.40

policy = vi.getPolicy(gridworld04, values, 1)
gridworld04.printPolicy(policy)

reward = -2
print("Grid World with additive rewards = %.2f\n" % reward)
gridworld2 = GridWorldEnv((3, 4), 0.8, [(1, 1)], terminals, reward)
values = vi.valueIteration(gridworld2, 1, 100)
gridworld2.printValues(values)
# q_values = vi.getQValues(gridworld2, values, 1)
# gridworld2.printQValues(q_values)

Grid World with additive rewards = -2.00

policy = vi.getPolicy(gridworld2, values, 1)
gridworld2.printPolicy(policy)

Reference

[1] Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction. MIT press, 2018.
[2] Sauer, Timothy. Numerical analysis. Pearson, 2018.
[3] https://github.com/ShangtongZhang/reinforcement-learning-an-introduction