Chapter 6 Temporal-Difference Learning
“Reinforcement Learning: An Introduction” by Richard Sutton & Andrew Barto, 2nd Ed
Author: Charles Zhang
All Notes Catelog for Reinforcement Learning: An Introduction. This post is created following BY-NC-ND 4.0 agreement, please follow terms while sharing.
Implementation for Exercises and Figures in the Book¶

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
from tqdm import tqdm
import copy
# 0 is the left terminal state
# 6 is the right terminal state
# 1 ... 5 represents A ... E
VALUES = np.zeros(7)
VALUES[1:6] = 0.5
# For convenience, we assume all rewards are 0
# and the left terminal state has value 0, the right terminal state has value 1
# This trick has been used in Gambler's Problem
VALUES[6] = 1
# set up true state values
TRUE_VALUE = np.zeros(7)
TRUE_VALUE[1:6] = np.arange(1, 6) / 6.0
TRUE_VALUE[6] = 1
ACTION_LEFT = 0
ACTION_RIGHT = 1
# @values: current states value, will be updated if @batch is False
# @alpha: step size
# @batch: whether to update @values
def temporal_difference(values, alpha=0.1, batch=False):
state = 3
trajectory = [state]
rewards = [0]
while True:
old_state = state
if np.random.binomial(1, 0.5) == ACTION_LEFT:
state -= 1
else:
state += 1
# Assume all rewards are 0
reward = 0
trajectory.append(state)
# TD update
if not batch:
values[old_state] += alpha * (reward + values[state] - values[old_state])
if state == 6 or state == 0:
break
rewards.append(reward)
return trajectory, rewards
# @values: current states value, will be updated if @batch is False
# @alpha: step size
# @batch: whether to update @values
def monte_carlo(values, alpha=0.1, batch=False):
state = 3
trajectory = [3]
# if end up with left terminal state, all returns are 0
# if end up with right terminal state, all returns are 1
while True:
if np.random.binomial(1, 0.5) == ACTION_LEFT:
state -= 1
else:
state += 1
trajectory.append(state)
if state == 6:
returns = 1.0
break
elif state == 0:
returns = 0.0
break
if not batch:
for state_ in trajectory[:-1]:
# MC update
values[state_] += alpha * (returns - values[state_])
return trajectory, [returns] * (len(trajectory) - 1)
# Example 6.2 left
def compute_state_value():
episodes = [0, 1, 10, 100]
current_values = np.copy(VALUES)
plt.figure(1)
for i in range(episodes[-1] + 1):
if i in episodes:
plt.plot(current_values, label=str(i) + ' episodes')
temporal_difference(current_values)
plt.plot(TRUE_VALUE, label='true values')
plt.xlabel('state')
plt.ylabel('estimated value')
plt.legend()
# Example 6.2 right
def rms_error():
# Same alpha value can appear in both arrays
td_alphas = [0.15, 0.1, 0.05]
mc_alphas = [0.01, 0.02, 0.03, 0.04]
episodes = 100 + 1
runs = 100
for i, alpha in enumerate(td_alphas + mc_alphas):
total_errors = np.zeros(episodes)
if i < len(td_alphas):
method = 'TD'
linestyle = 'solid'
else:
method = 'MC'
linestyle = 'dashdot'
for r in tqdm(range(runs)):
errors = []
current_values = np.copy(VALUES)
for i in range(0, episodes):
errors.append(np.sqrt(np.sum(np.power(TRUE_VALUE - current_values, 2)) / 5.0))
if method == 'TD':
temporal_difference(current_values, alpha=alpha)
else:
monte_carlo(current_values, alpha=alpha)
total_errors += np.asarray(errors)
total_errors /= runs
plt.plot(total_errors, linestyle=linestyle, label=method + ', alpha = %.02f' % (alpha))
plt.xlabel('episodes')
plt.ylabel('RMS')
plt.legend()
# Figure 6.2
# @method: 'TD' or 'MC'
def batch_updating(method, episodes, alpha=0.001):
# perform 100 independent runs
runs = 100
total_errors = np.zeros(episodes)
for r in tqdm(range(0, runs)):
current_values = np.copy(VALUES)
errors = []
# track shown trajectories and reward/return sequences
trajectories = []
rewards = []
for ep in range(episodes):
if method == 'TD':
trajectory_, rewards_ = temporal_difference(current_values, batch=True)
else:
trajectory_, rewards_ = monte_carlo(current_values, batch=True)
trajectories.append(trajectory_)
rewards.append(rewards_)
while True:
# keep feeding our algorithm with trajectories seen so far until state value function converges
updates = np.zeros(7)
for trajectory_, rewards_ in zip(trajectories, rewards):
for i in range(0, len(trajectory_) - 1):
if method == 'TD':
updates[trajectory_[i]] += rewards_[i] + current_values[trajectory_[i + 1]] - current_values[trajectory_[i]]
else:
updates[trajectory_[i]] += rewards_[i] - current_values[trajectory_[i]]
updates *= alpha
if np.sum(np.abs(updates)) < 1e-3:
break
# perform batch updating
current_values += updates
# calculate rms error
errors.append(np.sqrt(np.sum(np.power(current_values - TRUE_VALUE, 2)) / 5.0))
total_errors += np.asarray(errors)
total_errors /= runs
return total_errors
def example_6_2():
plt.figure(figsize=(6, 9))
plt.subplot(2, 1, 1)
compute_state_value()
plt.subplot(2, 1, 2)
rms_error()
plt.tight_layout()
plt.plot()
example_6_2()
def figure_6_2():
episodes = 100 + 1
td_erros = batch_updating('TD', episodes)
mc_erros = batch_updating('MC', episodes)
plt.plot(td_erros, label='TD')
plt.plot(mc_erros, label='MC')
plt.xlabel('episodes')
plt.ylabel('RMS error')
plt.legend()
plt.plot()
figure_6_2()
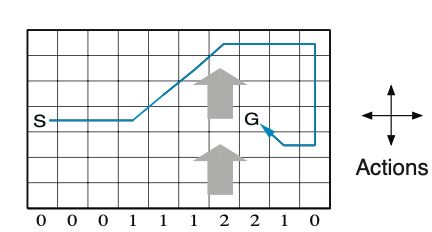
Example 6.5: Windy Gridworld Shown inset below is a standard gridworld, with start and goal states, but with one difference: there is a crosswind running upward through the middle of the grid. The actions are the standard four: up, down, right, and left—but in the middle region the resultant next states are shifted upward by a “wind,” the strength of which varies from column to column. The strength of the wind is given below each column, in number of cells shifted upward. For example, if you are one cell to the right of the goal, then the action left takes you to the cell just above the goal. This is an undiscounted episodic task, with constant rewards of $-1$ until the goal state is reached.
# world height
WORLD_HEIGHT = 7
# world width
WORLD_WIDTH = 10
# wind strength for each column
WIND = [0, 0, 0, 1, 1, 1, 2, 2, 1, 0]
# possible actions
ACTION_UP = 0
ACTION_DOWN = 1
ACTION_LEFT = 2
ACTION_RIGHT = 3
# probability for exploration
EPSILON = 0.1
# Sarsa step size
ALPHA = 0.5
# reward for each step
REWARD = -1.0
START = [3, 0]
GOAL = [3, 7]
ACTIONS = [ACTION_UP, ACTION_DOWN, ACTION_LEFT, ACTION_RIGHT]
def step(state, action):
i, j = state
if action == ACTION_UP:
return [max(i - 1 - WIND[j], 0), j]
elif action == ACTION_DOWN:
return [max(min(i + 1 - WIND[j], WORLD_HEIGHT - 1), 0), j]
elif action == ACTION_LEFT:
return [max(i - WIND[j], 0), max(j - 1, 0)]
elif action == ACTION_RIGHT:
return [max(i - WIND[j], 0), min(j + 1, WORLD_WIDTH - 1)]
else:
assert False
# play for an episode
def episode(q_value):
# track the total time steps in this episode
time = 0
# initialize state
state = START
# choose an action based on epsilon-greedy algorithm
if np.random.binomial(1, EPSILON) == 1:
action = np.random.choice(ACTIONS)
else:
values_ = q_value[state[0], state[1], :]
action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
# keep going until get to the goal state
while state != GOAL:
next_state = step(state, action)
if np.random.binomial(1, EPSILON) == 1:
next_action = np.random.choice(ACTIONS)
else:
values_ = q_value[next_state[0], next_state[1], :]
next_action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
# Sarsa update
q_value[state[0], state[1], action] += \
ALPHA * (REWARD + q_value[next_state[0], next_state[1], next_action] -
q_value[state[0], state[1], action])
state = next_state
action = next_action
time += 1
return time
def example_6_5():
q_value = np.zeros((WORLD_HEIGHT, WORLD_WIDTH, 4))
episode_limit = 500
steps = []
ep = 0
while ep < episode_limit:
steps.append(episode(q_value))
# time = episode(q_value)
# episodes.extend([ep] * time)
ep += 1
steps = np.add.accumulate(steps)
plt.plot(steps, np.arange(1, len(steps) + 1))
plt.xlabel('Time steps')
plt.ylabel('Episodes')
plt.plot()
# display the optimal policy
optimal_policy = []
for i in range(0, WORLD_HEIGHT):
optimal_policy.append([])
for j in range(0, WORLD_WIDTH):
if [i, j] == GOAL:
optimal_policy[-1].append('G')
continue
bestAction = np.argmax(q_value[i, j, :])
if bestAction == ACTION_UP:
optimal_policy[-1].append('U')
elif bestAction == ACTION_DOWN:
optimal_policy[-1].append('D')
elif bestAction == ACTION_LEFT:
optimal_policy[-1].append('L')
elif bestAction == ACTION_RIGHT:
optimal_policy[-1].append('R')
print('Optimal policy is:')
for row in optimal_policy:
print(row)
print('Wind strength for each column:\n{}'.format([str(w) for w in WIND]))
example_6_5()
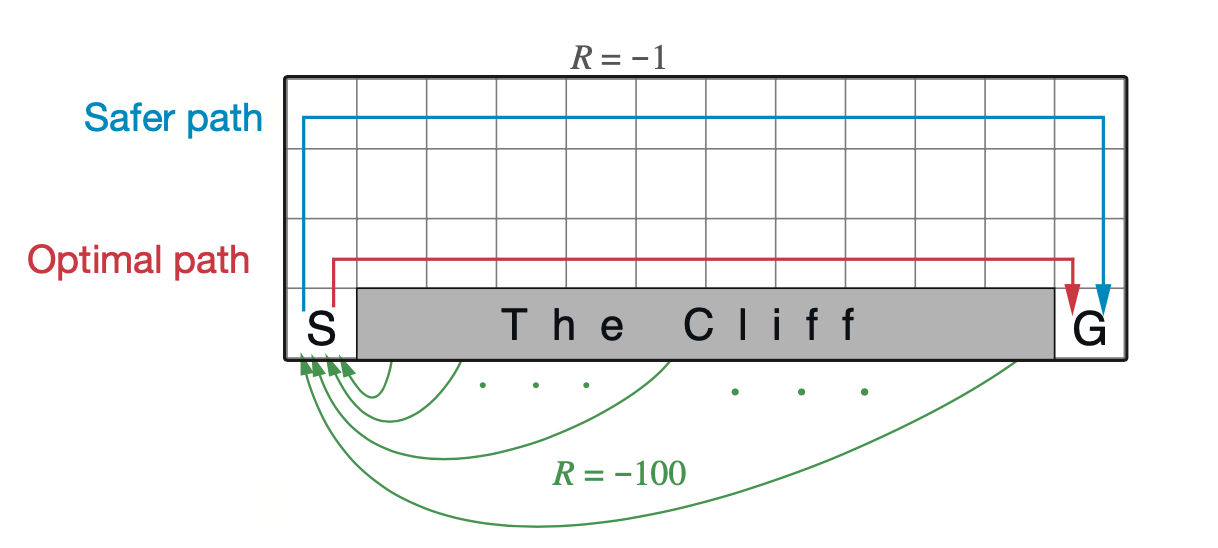
Example 6.6: Cliff Walking This gridworld example compares Sarsa and Q-learning, highlighting the difference between on-policy (Sarsa) and off-policy (Q-learning) methods. Consider the gridworld shown to the right. This is a standard undiscounted, episodic task, with start SaferRpath and goal states, and the usual actions causing movement up, down, Optimal path right, and left. Reward is $-1$ on all transitions except those into the region marked “The Cliff.” Stepping into this region incurs a reward of $-100$ and sends the agent instantly back to the start.
# world height
WORLD_HEIGHT = 4
# world width
WORLD_WIDTH = 12
# probability for exploration
EPSILON = 0.1
# step size
ALPHA = 0.5
# gamma for Q-Learning and Expected Sarsa
GAMMA = 1
# all possible actions
ACTION_UP = 0
ACTION_DOWN = 1
ACTION_LEFT = 2
ACTION_RIGHT = 3
ACTIONS = [ACTION_UP, ACTION_DOWN, ACTION_LEFT, ACTION_RIGHT]
# initial state action pair values
START = [3, 0]
GOAL = [3, 11]
def step(state, action):
i, j = state
if action == ACTION_UP:
next_state = [max(i - 1, 0), j]
elif action == ACTION_LEFT:
next_state = [i, max(j - 1, 0)]
elif action == ACTION_RIGHT:
next_state = [i, min(j + 1, WORLD_WIDTH - 1)]
elif action == ACTION_DOWN:
next_state = [min(i + 1, WORLD_HEIGHT - 1), j]
else:
assert False
reward = -1
if (action == ACTION_DOWN and i == 2 and 1 <= j <= 10) or (
action == ACTION_RIGHT and state == START):
reward = -100
next_state = START
return next_state, reward
# choose an action based on epsilon greedy algorithm
def choose_action(state, q_value):
if np.random.binomial(1, EPSILON) == 1:
return np.random.choice(ACTIONS)
else:
values_ = q_value[state[0], state[1], :]
return np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
# an episode with Sarsa
# @q_value: values for state action pair, will be updated
# @expected: if True, will use expected Sarsa algorithm
# @step_size: step size for updating
# @return: total rewards within this episode
def sarsa(q_value, expected=False, step_size=ALPHA):
state = START
action = choose_action(state, q_value)
rewards = 0.0
while state != GOAL:
next_state, reward = step(state, action)
next_action = choose_action(next_state, q_value)
rewards += reward
if not expected:
target = q_value[next_state[0], next_state[1], next_action]
else:
# calculate the expected value of new state
target = 0.0
q_next = q_value[next_state[0], next_state[1], :]
best_actions = np.argwhere(q_next == np.max(q_next))
for action_ in ACTIONS:
if action_ in best_actions:
target += ((1.0 - EPSILON) / len(best_actions) + EPSILON / len(ACTIONS)) * q_value[next_state[0], next_state[1], action_]
else:
target += EPSILON / len(ACTIONS) * q_value[next_state[0], next_state[1], action_]
target *= GAMMA
q_value[state[0], state[1], action] += step_size * (
reward + target - q_value[state[0], state[1], action])
state = next_state
action = next_action
return rewards
# an episode with Q-Learning
# @q_value: values for state action pair, will be updated
# @step_size: step size for updating
# @return: total rewards within this episode
def q_learning(q_value, step_size=ALPHA):
state = START
rewards = 0.0
while state != GOAL:
action = choose_action(state, q_value)
next_state, reward = step(state, action)
rewards += reward
# Q-Learning update
q_value[state[0], state[1], action] += step_size * (
reward + GAMMA * np.max(q_value[next_state[0], next_state[1], :]) -
q_value[state[0], state[1], action])
state = next_state
return rewards
# print optimal policy
def print_optimal_policy(q_value):
optimal_policy = []
for i in range(0, WORLD_HEIGHT):
optimal_policy.append([])
for j in range(0, WORLD_WIDTH):
if [i, j] == GOAL:
optimal_policy[-1].append('G')
continue
bestAction = np.argmax(q_value[i, j, :])
if bestAction == ACTION_UP:
optimal_policy[-1].append('U')
elif bestAction == ACTION_DOWN:
optimal_policy[-1].append('D')
elif bestAction == ACTION_LEFT:
optimal_policy[-1].append('L')
elif bestAction == ACTION_RIGHT:
optimal_policy[-1].append('R')
for row in optimal_policy:
print(row)
# Use multiple runs instead of a single run and a sliding window
# With a single run I failed to present a smooth curve
# However the optimal policy converges well with a single run
# Sarsa converges to the safe path, while Q-Learning converges to the optimal path
def example_6_6():
# episodes of each run
episodes = 500
# perform 40 independent runs
runs = 50
rewards_sarsa = np.zeros(episodes)
rewards_q_learning = np.zeros(episodes)
for r in tqdm(range(runs)):
q_sarsa = np.zeros((WORLD_HEIGHT, WORLD_WIDTH, 4))
q_q_learning = np.copy(q_sarsa)
for i in range(0, episodes):
# cut off the value by -100 to draw the figure more elegantly
# rewards_sarsa[i] += max(sarsa(q_sarsa), -100)
# rewards_q_learning[i] += max(q_learning(q_q_learning), -100)
rewards_sarsa[i] += sarsa(q_sarsa)
rewards_q_learning[i] += q_learning(q_q_learning)
# averaging over independt runs
rewards_sarsa /= runs
rewards_q_learning /= runs
# draw reward curves
plt.plot(rewards_sarsa, label='Sarsa')
plt.plot(rewards_q_learning, label='Q-Learning')
plt.xlabel('Episodes')
plt.ylabel('Sum of rewards during episode')
plt.ylim([-100, 0])
plt.legend()
plt.plot()
# display optimal policy
print('Sarsa Optimal Policy:')
print_optimal_policy(q_sarsa)
print('Q-Learning Optimal Policy:')
print_optimal_policy(q_q_learning)
example_6_6()
Interim and asymptotic performance of TD control methods on the cliff-walking task as a function of $\alpha$.¶
# Due to limited capacity of calculation of my machine, I can't complete this experiment
# with 100,000 episodes and 50,000 runs to get the fully averaged performance
# However even I only play for 1,000 episodes and 10 runs, the curves looks still good.
def figure_6_3():
step_sizes = np.arange(0.1, 1.1, 0.1)
episodes = 1000
runs = 10
ASY_SARSA = 0
ASY_EXPECTED_SARSA = 1
ASY_QLEARNING = 2
INT_SARSA = 3
INT_EXPECTED_SARSA = 4
INT_QLEARNING = 5
methods = range(0, 6)
performace = np.zeros((6, len(step_sizes)))
for run in range(runs):
for ind, step_size in tqdm(list(zip(range(0, len(step_sizes)), step_sizes))):
q_sarsa = np.zeros((WORLD_HEIGHT, WORLD_WIDTH, 4))
q_expected_sarsa = np.copy(q_sarsa)
q_q_learning = np.copy(q_sarsa)
for ep in range(episodes):
sarsa_reward = sarsa(q_sarsa, expected=False, step_size=step_size)
expected_sarsa_reward = sarsa(q_expected_sarsa, expected=True, step_size=step_size)
q_learning_reward = q_learning(q_q_learning, step_size=step_size)
performace[ASY_SARSA, ind] += sarsa_reward
performace[ASY_EXPECTED_SARSA, ind] += expected_sarsa_reward
performace[ASY_QLEARNING, ind] += q_learning_reward
if ep < 100:
performace[INT_SARSA, ind] += sarsa_reward
performace[INT_EXPECTED_SARSA, ind] += expected_sarsa_reward
performace[INT_QLEARNING, ind] += q_learning_reward
performace[:3, :] /= episodes * runs
performace[3:, :] /= 100 * runs
labels = ['Asymptotic Sarsa', 'Asymptotic Expected Sarsa', 'Asymptotic Q-Learning',
'Interim Sarsa', 'Interim Expected Sarsa', 'Interim Q-Learning']
for method, label in zip(methods, labels):
plt.plot(step_sizes, performace[method, :], label=label)
plt.xlabel('alpha')
plt.ylabel('reward per episode')
plt.legend()
plt.plot()
figure_6_3()
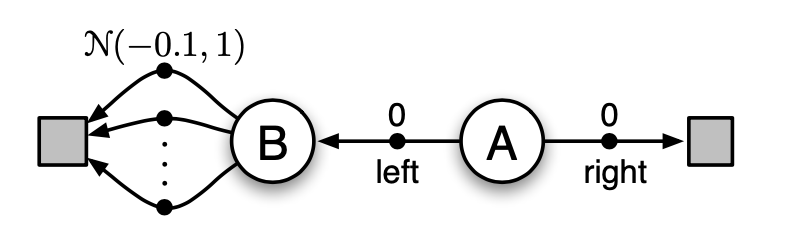
Example 6.7: Maximization Bias Example The small MDP shown inset in Figure below provides a simple example of how maximization bias can harm the performance of TD control algorithms. The MDP has two non-terminal states $A$ and $B$. Episodes always start in $A$ with a choice between two actions, left and right. The right action transitions immediately to the terminal state with a reward and return of zero. The left action transitions to $B$, also with a reward of zero, from which there are many possible actions all of which cause immediate termination with a reward drawn from a normal distribution with mean $0.1$ and variance $1.0$. Thus, the expected return for any trajectory starting with left is $0.1$, and thus taking left in state $A$ is always a mistake. Nevertheless, our control methods may favor left because of maximization bias making B appear to have a positive value.
# state A
STATE_A = 0
# state B
STATE_B = 1
# use one terminal state
STATE_TERMINAL = 2
# starts from state A
STATE_START = STATE_A
# possible actions in A
ACTION_A_RIGHT = 0
ACTION_A_LEFT = 1
# probability for exploration
EPSILON = 0.1
# step size
ALPHA = 0.1
# discount for max value
GAMMA = 1.0
# possible actions in B, maybe 10 actions
ACTIONS_B = range(0, 10)
# all possible actions
STATE_ACTIONS = [[ACTION_A_RIGHT, ACTION_A_LEFT], ACTIONS_B]
# state action pair values, if a state is a terminal state, then the value is always 0
INITIAL_Q = [np.zeros(2), np.zeros(len(ACTIONS_B)), np.zeros(1)]
# set up destination for each state and each action
TRANSITION = [[STATE_TERMINAL, STATE_B], [STATE_TERMINAL] * len(ACTIONS_B)]
# choose an action based on epsilon greedy algorithm
def choose_action(state, q_value):
if np.random.binomial(1, EPSILON) == 1:
return np.random.choice(STATE_ACTIONS[state])
else:
values_ = q_value[state]
return np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
# take @action in @state, return the reward
def take_action(state, action):
if state == STATE_A:
return 0
return np.random.normal(-0.1, 1)
# if there are two state action pair value array, use double Q-Learning
# otherwise use normal Q-Learning
def q_learning(q1, q2=None):
state = STATE_START
# track the # of action left in state A
left_count = 0
while state != STATE_TERMINAL:
if q2 is None:
action = choose_action(state, q1)
else:
# derive a action form Q1 and Q2
action = choose_action(state, [item1 + item2 for item1, item2 in zip(q1, q2)])
if state == STATE_A and action == ACTION_A_LEFT:
left_count += 1
reward = take_action(state, action)
next_state = TRANSITION[state][action]
if q2 is None:
active_q = q1
target = np.max(active_q[next_state])
else:
if np.random.binomial(1, 0.5) == 1:
active_q = q1
target_q = q2
else:
active_q = q2
target_q = q1
best_action = np.random.choice([action_ for action_, value_ in enumerate(active_q[next_state]) if value_ == np.max(active_q[next_state])])
target = target_q[next_state][best_action]
# Q-Learning update
active_q[state][action] += ALPHA * (
reward + GAMMA * target - active_q[state][action])
state = next_state
return left_count
# Figure 6.7, 1,000 runs may be enough, # of actions in state B will also affect the curves
def figure_6_5():
# each independent run has 300 episodes
episodes = 300
runs = 1000
left_counts_q = np.zeros((runs, episodes))
left_counts_double_q = np.zeros((runs, episodes))
for run in tqdm(range(runs)):
q = copy.deepcopy(INITIAL_Q)
q1 = copy.deepcopy(INITIAL_Q)
q2 = copy.deepcopy(INITIAL_Q)
for ep in range(0, episodes):
left_counts_q[run, ep] = q_learning(q)
left_counts_double_q[run, ep] = q_learning(q1, q2)
left_counts_q = left_counts_q.mean(axis=0)
left_counts_double_q = left_counts_double_q.mean(axis=0)
plt.plot(left_counts_q, label='Q-Learning')
plt.plot(left_counts_double_q, label='Double Q-Learning')
plt.plot(np.ones(episodes) * 0.05, label='Optimal')
plt.xlabel('episodes')
plt.ylabel('% left actions from A')
plt.legend()
plt.plot()
figure_6_5()
import random
import numpy as np
from matplotlib.table import Table
import matplotlib.pyplot as plt
from collections import defaultdict
from collections import Counter
import tqdm
"""
--------------------------
Environment
c 0 1 2 3
r - - - - - - - - - -
0 | | | | +1 |
- - - - - - - - - -
1 | |WALL| | -1 |
- - - - - - - - - -
2 | | | | |
- - - - - - - - - -
For Visualization:
- - - - - - - - - -
3 | | | | +1 |
- - - - - - - - - -
2 | |WALL| | -1 |
- - - - - - - - - -
1 | | | | |
r - - - - - - - - - -
c 1 2 3 4
@author: Charles Zhang
@date Mar 28, 2021
---------------------------
"""
# Grid Environment for MDP Value Iteration
class GridWorldEnv:
START = (0, 0)
EXIT = (float("inf"), float("inf"))
# actions
NORTH = (-1, 0)
EAST = (0, 1)
SOUTH = (1, 0)
WEST = (0, -1)
ACTIONS = [NORTH, EAST, SOUTH, WEST]
index = {NORTH: 0, EAST: 1, SOUTH: 2, WEST: 3, EXIT: -1}
GAMEOVER = (-1, -1) # by convenience, the next state of terminals is (-1, -1)
def __init__(self, shape, prob, walls, terminals, alive_reward=0.0):
"""
:param shape: shape of gridworld: (row, col)
:param prob: probability to go north(for stochastic move)
:param walls: list of walls: [(1, 1)] if only one wall at (1, 1)
:param terminals: dictionary of goal and death terminal states with reward
{(0, 3): +1, (1, 3): -1} in this problem
:param alive_reward: alive reward
"""
self.rows, self.cols = shape
p_not_north = (1 - prob) / 2
self.turns = {-1: p_not_north, 0: prob, 1: p_not_north} # turn west, north, or east
self.walls = set(walls)
self.terminals = terminals
self.alive_reward = alive_reward
self.state = self.START
def reset(self):
self.state = self.START
def step(self, action):
state = self.state
if action == self.EXIT:
self.state = self.GAMEOVER
return self.getReward(state, action, state), self.state
direction = action
prob, accident = self.turns[0], self.turns[1]
if prob <= random.random() < prob + accident:
direction = self.ACTIONS[(self.index[action] - 1) % len(self.ACTIONS)]
elif random.random() >= prob + accident:
direction = self.ACTIONS[(self.index[action] + 1) % len(self.ACTIONS)]
row = state[0] + direction[0]
col = state[1] + direction[1]
next_state = (row if 0 <= row < self.rows else state[0],
col if 0 <= col < self.cols else state[1])
if next_state in self.walls:
next_state = state
self.state = next_state
return self.getReward(state, action, self.state), self.state
def getStates(self):
"""
All available states(all states except wall(s))
"""
return [(i, j) for i in range(self.rows)
for j in range(self.cols) if (i, j) not in self.walls]
def getTransitionStatesAndProbs(self, state, action):
"""
get all (next state, p(s' | s, a)), in terms of stochastic action
:return: list of (next_state, probability to the next state given current state and action)
"""
if state in self.terminals:
# if the state is terminal state, the probability of game over is 1
return [(GridWorldEnv.GAMEOVER, 1.0)]
result = []
for turn in self.turns: # loop over all turns(west, north, east)
# turn west, north, or east of the "planned" action for the "real" action
# -1, 0, 1, or 2 % 4 to get the "real" tuple of direction(action), e.g.:
# planned: EAST, index 1 => turn is WEST(of EAST), index -1 => 1 + -1 = 0 => mod 4 => 0: real action NORTH
# => turn is NORTH(of EAST), index 0 => 1 + 0 = 1 => mod 4 => 1: real action EAST
direction = GridWorldEnv.ACTIONS[(GridWorldEnv.index[action] + turn) % len(GridWorldEnv.ACTIONS)]
row = state[0] + direction[0] # x coordinate of next state
col = state[1] + direction[1] # y coordinate of next state
next_state = (row if 0 <= row < self.rows else state[0],
col if 0 <= col < self.cols else state[1]) # possible next state considered wall(s)
if next_state in self.walls: # stay if is wall
next_state = state
prob = self.turns[turn]
result.append((next_state, prob))
return result
def getReward(self, state, action, nextState):
"""
r(s, a, s')
"""
if state in self.terminals:
return self.terminals[state] # get reward(penalty) for terminal states
else:
return self.alive_reward # alive exploration rewards
@staticmethod
def isTerminal(next_state):
"""
check if next state is terminal state, and by convenience, the next state of terminals is (-1, -1)
"""
return next_state == GridWorldEnv.GAMEOVER
def getLegalActions(self, state):
"""
get all possible actions, if state the terminal, by convenience return (INF, INF)
"""
if state in self.terminals:
return [GridWorldEnv.EXIT]
else:
return GridWorldEnv.ACTIONS
def to_2d_array(self, in_list, add=None):
"""
input list to 2D array(matrix) based on rows and columns
"""
mat = []
k = False
for i in range(self.rows):
temp = []
for j in range(self.cols):
if add is not None:
if (i, j) in self.walls:
temp.append(add)
k = True
continue
if k:
temp.append(in_list[i * self.cols + j - 1])
else:
temp.append(in_list[i * self.cols + j])
mat.append(temp)
return mat
def printValues(self, values):
"""
visualize values in a table
"""
fig, ax = plt.subplots()
ax.set_axis_off()
tb = Table(ax, bbox=[0, 0, 1, 1])
values = list(values.values())
values = np.round(np.array(self.to_2d_array(values, add=0)), decimals=2)
width, height = 1.0 / self.rows, 1.0 / self.cols
# Add cells
for (i, j), val in np.ndenumerate(values):
tb.add_cell(i, j, width, height, text=val,
loc='center', facecolor='white')
# Row and column labels...
n = max(self.rows, self.cols)
for i in range(n):
if i < self.rows:
tb.add_cell(i, -1, width, height, text=self.rows - i, loc='right',
edgecolor='none', facecolor='none')
if i < self.cols:
tb.add_cell(self.rows, i, width, height / 2, text=i + 1, loc='center',
edgecolor='none', facecolor='none')
tb.set_fontsize(13)
ax.add_table(tb)
plt.plot()
def printQValues(self, q_values):
fig, ax = plt.subplots()
ax.set_axis_off()
tb = Table(ax, bbox=[0, 0, 1, 1])
width, height = 1.0 / self.rows, 1.0 / self.cols
qs = []
for i in range(self.rows):
for j in range(self.cols):
q = ''
if (i, j) in self.walls or (i, j) in list(self.terminals.keys()):
q += " \n"
else:
q += " %.2f \n" % (q_values[(i, j), GridWorldEnv.NORTH])
if (i, j) in self.walls:
q += " \n"
elif (i, j) in self.terminals:
q += " %.2f \n" % q_values[(i, j), GridWorldEnv.EXIT]
else:
q += "%.2f %.2f\n" % (q_values[(i, j), GridWorldEnv.WEST], q_values[(i, j), GridWorldEnv.EAST])
if (i, j) in self.walls or (i, j) in list(self.terminals.keys()):
q += " "
else:
q += " %.2f " % (q_values[(i, j), GridWorldEnv.SOUTH])
qs.append(q)
qs = self.to_2d_array(qs)
qs = np.array(qs)
for (i, j), q in np.ndenumerate(qs):
tb.add_cell(i, j, width, height, text=q,
loc='center', facecolor='white')
n = max(self.rows, self.cols)
for i in range(n):
if i < self.rows:
tb.add_cell(i, -1, width, height, text=self.rows - i, loc='right',
edgecolor='none', facecolor='none')
if i < self.cols:
tb.add_cell(self.rows, i, width, height / 2, text=i + 1, loc='center',
edgecolor='none', facecolor='none')
tb.set_fontsize(15)
ax.add_table(tb)
plt.plot()
def printPolicy(self, policy):
action_map = {0: '↑', 1: '→',
2: '↓', 3: '←',
-1: ' '}
policy = list(policy.values())
policy = self.to_2d_array(policy, add=-1)
policy = np.array(policy, dtype=object)
fig, ax = plt.subplots()
ax.set_axis_off()
tb = Table(ax, bbox=[0, 0, 1, 1])
width, height = 1.0 / self.rows, 1.0 / self.cols
for (i, j), action in np.ndenumerate(policy):
if (i, j) in self.walls:
tb.add_cell(i, j, width, height, text='',
loc='center', facecolor='gray')
elif (i, j) == list(self.terminals.keys())[0]:
tb.add_cell(i, j, width, height, text='+1',
loc='center', facecolor='blue')
elif (i, j) == list(self.terminals.keys())[1]:
tb.add_cell(i, j, width, height, text='-1',
loc='center', facecolor='red')
else:
tb.add_cell(i, j, width, height, text=action_map[action],
loc='center', facecolor='white')
n = max(self.rows, self.cols)
for i in range(n):
if i < self.rows:
tb.add_cell(i, -1, width, height, text=self.rows - i, loc='right',
edgecolor='none', facecolor='none')
if i < self.cols:
tb.add_cell(self.rows, i, width, height / 2, text=i + 1, loc='center',
edgecolor='none', facecolor='none')
tb.set_fontsize(13)
ax.add_table(tb)
plt.plot()
Value Iteration Method for $V_*$¶
"""
--------------------------------------------------------------------------------------
Bellman Equation:
v(s) = Σ_{a} π(a | s) Σ_{s', r} p(s', r | s, a) * [r + γ * v(s')]
Bellman Optimality Equation:
v*(s) = max_{a} { Σ p(s', r | s, a) * [r + γ * v(s')] }
= max q_{π*} (s, a) = max q(s, a), as π(a | s) is unchanged in this MDP problem
@author: Charles Zhang
@date Mar 28, 2021
--------------------------------------------------------------------------------------
"""
# MDP Value Iteration with Bellman update
class ValueIteration:
"""
Class to Find Optimal Value Functions
"""
def valueIteration(self, GridWorld, discount=0.9, iterations=100):
"""
Implement the value iteration algorithm by the optimal value function derived by Bellman equation
v*(s) = max q(s, a)
:param GridWorld: gridworld environment
:param discount: discount gamma
:param iterations: iteration times
:return dictionary of values of all states
"""
values = defaultdict(lambda: 0) # initialize values with all 0 of states
for i in range(iterations): # or while TRUE:
vnext = defaultdict(lambda: 0) # initialize values for each iteration with all 0 of states
for state in GridWorld.getStates(): # loop over all possible state(all states except wall(s))
if not GridWorld.isTerminal(state): # check if the state is terminal
maximum = float("-inf")
for action in GridWorld.getLegalActions(state): # loop over all possible actions
q_value = self.get_q_from_v(GridWorld, state, action, values, discount)
maximum = max(maximum, q_value) # update the max q value among actions of current state
vnext[state] = maximum # optimal v*(s) = max q(s, a)
values = vnext # update the new value table
# if while TURE above, here could compare the difference between
# values and vnext to see if converges, and end the loop
return values
@staticmethod
def get_q_from_v(GridWorld, state, action, values, discount=0.9):
"""
get q(s, a) from values v(s) and action a by
Bellman Equation: q(s, a) = Σ p(s', r | s, a) * [r + γ * v(s')]
:param GridWorld: gridworld environment
:param state: current state s
:param action: current selected action a
:param values: current values table
:param discount: discount gamma
:return: float q(s, a)
"""
q_val = 0
# implement Bellman equation: q(s, a) = Σ p(s', r | s, a) * [r + γ * v(s')]
for next_state, prob in GridWorld.getTransitionStatesAndProbs(state, action):
q_val += prob * (GridWorld.getReward(state, action, next_state) + discount * values[next_state])
return q_val
def getQValues(self, GridWorld, values, discount=0.9):
"""
Get q values by Values
:return dictionary of q values of all states
"""
q_values = {}
for state in GridWorld.getStates():
if not GridWorld.isTerminal(state):
for action in GridWorld.getLegalActions(state):
q_values[state, action] = self.get_q_from_v(GridWorld, state, action, values, discount)
return q_values
def getPolicy(self, GridWorld, values, discount=0.9):
"""
get policy by values
π*(s) ≈ π(s) = argmax_a Σ p(s', r | s, a) * [r + γ * v(s')] = argmax_a q(s, a)
:return dictionary of optimal actions of all states
"""
policy = {}
for state in GridWorld.getStates():
if not GridWorld.isTerminal(state):
maximum = -float("inf")
best_action = None
# Choose action for the policy based no the max q values among actions of state s
for action in GridWorld.getLegalActions(state):
q_value = self.get_q_from_v(GridWorld, state, action, values, discount)
if q_value > maximum:
maximum = q_value
best_action = action
best_action = GridWorld.index[best_action]
policy[state] = best_action
return policy
Solve GridWorld¶
gamma = 0.9
alive_reward = 0
print("GridWorld Value Iteration with alive reward = %.2f, discount gamma = %.2f\n" % (alive_reward, gamma))
terminals = {(0, 3): 1, (1, 3): -1}
gridworld0 = GridWorldEnv(shape=(3, 4), prob=0.8, walls=[(1, 1)], terminals=terminals, alive_reward=alive_reward)
vi = ValueIteration()
values = vi.valueIteration(GridWorld=gridworld0, discount=gamma, iterations=500)
gridworld0.printValues(values)
q_values = vi.getQValues(GridWorld=gridworld0, values=values, discount=gamma)
gridworld0.printQValues(q_values)
policy = vi.getPolicy(GridWorld=gridworld0, values=values, discount=gamma)
gridworld0.printPolicy(policy)
TD Learning¶
"""
--------------------------------------------------------------------------------------
Temporal Difference Methods including TD(0), SARSA, Q Learning, and Double Q learning
Algorithm to approximate the optimal policy v*, q*, π*, and q* respectively.
Also verified by sum of rewards of each epsidoe, and RMSE with the optimal Q values,
approximated by q values derived by value iteration using optimal Bellman Equation.
@author: Charles Zhang
@date Apr 14, 2021
--------------------------------------------------------------------------------------
"""
class TD:
"""
Base Temporal Difference Learning Agent
"""
def __init__(self, env, alpha=0.1, gamma=0.9, epsilon=0.3):
self.env = env
self.alpha = alpha
self.gamma = gamma
self.epsilon = epsilon
self.qvalues = defaultdict(lambda: 0)
self.rmse = []
def getAction(self, state):
"""
Implement the epsilon-greedy method
"""
if np.random.binomial(1, self.epsilon) == 1:
return random.choice(self.env.getLegalActions(state))
# if random.random() < self.epsilon:
# return random.choice(self.env.getLegalActions(state))
else:
return self.getPolicy(state)
def getPolicy(self, state):
"""
choose the action of the max_a q(s, a)
"""
actions = self.env.getLegalActions(state)
return max(actions, key=lambda action: self.qvalues[state, action])
def get_expected_q(self):
"""
approximated expected q derived by value iteration algorithm
"""
vi = ValueIteration()
values = vi.valueIteration(self.env, discount=self.gamma, iterations=5000)
return vi.getQValues(GridWorld=self.env, values=values, discount=gamma)
@staticmethod
def getRMSError(expect, result):
"""
Root Mean Square Error
"""
sumSE = 0
for key in expect:
sumSE += (expect[key] - result[key]) ** 2
MSE = sumSE / len(expect)
return MSE ** 0.5
TD(0)¶
class TDZero:
def __init__(self, env, policy, alpha=0.3, gamma=0.9):
self.env = env
self.policy = policy
self.alpha = alpha
self.gamma = gamma
self.v = {s: 0 for s in self.env.getStates()}
self.v[(-1, -1)] = 0
self.rmse = []
@staticmethod
def getAction(state, policy):
"""
get the action based on input policy
"""
prob_a = policy[state]
actions = list(prob_a.keys())
return actions[np.random.choice(a=len(actions), p=list(prob_a.values()))]
def td0(self, episodes=1000):
expected_v = vi.valueIteration(self.env, discount=self.gamma, iterations=1000)
for _ in tqdm.tqdm(range(episodes)):
self.env.reset()
while not self.env.isTerminal(self.env.state):
state = self.env.state
action = self.getAction(state, self.policy)
reward, next_state = self.env.step(action)
self.v[state] += self.alpha * (reward + self.gamma * self.v[next_state] - self.v[state])
error = self.getRMSError(expected_v, self.v)
self.rmse.append(error)
return self.v
@staticmethod
def getRMSError(expect, result):
sumSE = 0
ev = list(expect.values())
er = list(result.values())
for i in range(len(ev)):
sumSE += (ev[i] - er[i]) ** 2
MSE = sumSE / len(ev)
return MSE ** 0.5
# A policy to be evaluated: 0.7 for action corresponding with the optimal policy, 0.1 for the rest of actions
input_policy = {s: {a: 0.1 for a in gridworld0.getLegalActions(s)} for s in
gridworld0.getStates() if s not in gridworld0.terminals.keys()}
for s in gridworld0.terminals.keys():
input_policy[s] = {(float('inf'), float('inf')): 1}
vi = ValueIteration()
for s in policy.keys():
if s not in gridworld0.terminals.keys():
expected_a_index = policy[s]
expected_a = list(gridworld0.index.keys())[list(gridworld0.index.values()).index(expected_a_index)]
input_policy[s][expected_a] = 0.7
td0 = TDZero(gridworld0, policy=input_policy, alpha=0.1, gamma=gamma)
values = td0.td0(episodes=2000)
print("Values derived by TD(0) Method")
gridworld0.printValues(values)
values = vi.valueIteration(GridWorld=gridworld0, discount=gamma, iterations=500)
print("Values derived by Value Iteration Algorithm")
gridworld0.printValues(values)
rmse = td0.rmse
plt.plot(rmse)
plt.xlabel("Episodes")
plt.ylabel("RMS Error")
plt.show()
print(rmse[-1])
gridworld0.printPolicy(vi.getPolicy(gridworld0, values, discount=gamma))
print('TD(0) Policy: ')
SARSA¶
class SARSA(TD):
def sarsa(self, episodes=5000):
expected_q = self.get_expected_q()
for _ in tqdm.tqdm(range(episodes)):
self.env.reset() # Initialize S
state = self.env.state
action = self.getAction(state) # Choose A from S using policy derived from Q (e.g., eps greedy)
while not self.env.isTerminal(state):
reward, next_state = self.env.step(action) # Take action A, observe R, S'
next_action = self.getAction(next_state) # Choose A0 from S0 using policy derived from Q (e.g.,greedy)
diff = self.alpha * (reward +
self.gamma * self.qvalues[next_state, next_action] -
self.qvalues[state, action])
self.qvalues[state, action] += diff # SARSA TD update
state = next_state # S <- S'
action = next_action # A <- A'
error = self.getRMSError(expected_q, self.qvalues)
self.rmse.append(error)
policy = {s: self.env.index[self.getPolicy(s)] for s in self.env.getStates()}
return policy
sarsa = SARSA(gridworld0, alpha=0.1, gamma=gamma, epsilon=0.3)
policy = sarsa.sarsa(episodes=2000)
gridworld0.printPolicy(policy)
print('SARSA Policy: ')
rmse = sarsa.rmse
plt.plot(rmse)
plt.xlabel("Episodes")
plt.ylabel("RMS Error")
plt.show()
print('The Q values derived by value iteration')
gridworld0.printQValues(q_values)
print('The predicted optimal Q values by SARSA')
gridworld0.printQValues(sarsa.qvalues)
Q Learning¶
class QLearning(TD):
def q_learning(self, episodes=500):
expected_q = self.get_expected_q()
for _ in tqdm.tqdm(range(episodes)): # loop for each episode
self.env.reset() # Initialize S
while not self.env.isTerminal(self.env.state): # loop for each step of episode(can also use trajectories)
state = self.env.state # current state
action = self.getAction(state) # Choose A from S using policy derived from Q (e.g., epsilon-greedy)
reward, next_state = self.env.step(action) # Take action A, observe R, S'
next_actions = self.env.getLegalActions(next_state) # get legal next actions to compute max_a
diff = self.alpha * (reward +
self.gamma * max(self.qvalues[next_state, a] for a in next_actions) -
self.qvalues[state, action])
self.qvalues[state, action] += diff # temporal difference update
error = self.getRMSError(expected_q, self.qvalues) # store the RMS error per episode
self.rmse.append(error)
policy = {s: self.env.index[self.getPolicy(s)] for s in self.env.getStates()}
return policy
q = QLearning(gridworld0, alpha=0.2, gamma=gamma, epsilon=0.8)
policy = q.q_learning(episodes=1000)
print('Q Learning Policy: ')
gridworld0.printPolicy(policy)
rmse = q.rmse
plt.plot(rmse)
plt.xlabel("Episodes")
plt.ylabel("RMS Error")
plt.show()
print("The Last RMSE: %f" % (rmse[-1]))
print('The Q values derived by value iteration')
gridworld0.printQValues(q_values)
print('The predicted Q values by Q-learning')
gridworld0.printQValues(q.qvalues)
Double Q Learning¶
class DoubleQLearning(TD):
"""
Double Q-learning, for estimating Q1 ≈ Q2 ≈ q*
"""
def __init__(self, env, alpha=0.1, gamma=0.9, epsilon=0.3):
super().__init__(env, alpha, gamma, epsilon)
self.q1 = defaultdict(lambda: 0)
self.q2 = defaultdict(lambda: 0)
self.rmse1 = []
self.rmse2 = []
def getDoubleQPolicy(self, state):
"""
Choose A from S using greedy policy in Q1+Q2
"""
actions = self.env.getLegalActions(state)
return max(actions, key=lambda action: self.q1[state, action] + self.q2[state, action])
def double_q_learning(self, episodes=5000):
expected_q = self.get_expected_q()
for _ in tqdm.tqdm(range(episodes)): # loop for each episode
self.env.reset() # Initialize S
while not self.env.isTerminal(self.env.state): # loop for each step of episode
state = self.env.state # current state
action = self.getAction(state) # Choose A from S using greedy policy in Q1+Q2
reward, next_state = self.env.step(action) # Take action A, observe R, S'
if random.random() < 0.5: # With 0.5 probability
self.qvalues = self.q1
argmax_action = self.getPolicy(next_state) # best action for next state
diff = self.alpha * (reward +
self.gamma * self.q2[next_state, argmax_action] -
self.q1[state, action])
self.q1[state, action] += diff
else:
self.qvalues = self.q1
argmax_action = self.getPolicy(next_state) # best action for next state
diff = self.alpha * (reward +
self.gamma * self.q1[next_state, argmax_action] -
self.q2[state, action])
self.q2[state, action] += diff # temporal difference update
error1 = self.getRMSError(expected_q, self.q1) # store the Q1 RMS error per episode
self.rmse1.append(error1)
error2 = self.getRMSError(expected_q, self.q2) # store the Q2 RMS error per episode
self.rmse2.append(error2)
self.qvalues = self.q1
q1_policy = {s: self.env.index[self.getPolicy(s)] for s in self.env.getStates()}
self.qvalues = self.q2
q2_policy = {s: self.env.index[self.getPolicy(s)] for s in self.env.getStates()}
return q1_policy, q2_policy
dq = DoubleQLearning(gridworld0, alpha=0.1, gamma=gamma, epsilon=1)
q1_policy, q2_policy = dq.double_q_learning(episodes=2000)
print('Double Q Learning Policy derived by Q1: ')
gridworld0.printPolicy(q1_policy)
print('Double Q Learning Policy derived by Q2: ')
gridworld0.printPolicy(q2_policy)
rmse1 = dq.rmse1
plt.plot(rmse1)
plt.xlabel("Episodes")
plt.ylabel("RMS Error of Q1")
plt.show()
rmse2 = dq.rmse2
plt.plot(rmse2)
plt.xlabel("Episodes")
plt.ylabel("RMS Error of Q2")
print("The Last RMSE of Q1: %f" % (rmse1[-1]))
print("The Last RMSE of Q2: %f" % (rmse2[-1]))
print('The Q1 values derived by Double Q Learning')
gridworld0.printQValues(dq.q1)
print('The Q2 values derived by Double Q Learning')
gridworld0.printQValues(dq.q2)
print('The Q values derived by value iteration')
gridworld0.printQValues(q_values)
